Crib sheet

This is just a bunch of information that may or may not be useful on a crib sheet

1Datatypes¶

datatype for creating new, custom datatypes (e.g. datatype suit = Spades | Clubs | Hearts | Diamonds); type for aggregating existing types (e.g. type complex = int * int)

2Recursive functions¶

Anonymous functions can only be recursive if you use the rec keyword:

val rec factorial = fn 0 => 1 | n => n * factorial (n-1)

Otherwise, recursive functions can be implemented using the fun keyword:

fun factorial 0 = 1 | factorial n = n * factorial (n-1)

3Pattern matching¶

Can: tuples, constructors, lists, records (val {first, last} = {first="Ash", last="Ketchum"})
Cannot: non-constructor functions (e.g. !, str)

4Higher-order functions¶

• List.concat (@) - 'a list list -> 'a list
• List.map (map) - ('a -> 'b) -> 'a list -> 'b list
• List.filter - ('a -> bool) -> 'a list -> 'a list
• List.foldl - ('a * 'b -> 'b) -> 'b -> 'a list -> 'b list; starts from the left
• List.foldr - ('a * 'b -> 'b) -> 'b -> 'a list -> 'b list; starts from the right
• List.exists - ('a -> bool) -> 'a list -> bool
• List.all - ('a -> bool) -> 'a list -> bool
• curry - ((’a ’b) -> ’c) -> (’a -> ’b -> ’c) (code: fun curry f = (fn x => fn y => f (x,y)))
• uncurry - (’a -> ’b -> ’c) -> ((’a ’b) -> ’c) ) (code: fun uncurry f = (fn (y,x) => f y x))

5Lazy programming¶

SML is call-by-value - when we use val, we evaluate the expression before binding it etc (eager). Call-by-name doesn't evaluate it until it's used, but if it's used twice, it's evaluated twice etc. Lazy programming is call-by-name, but it memoises as well. Useful for generating things, like generators in python.

Uses continuations - doesn't actually call the function until you pass it to force (this works because you never evaluate inside a function body until it's actually applied)

datatype 'a susp = Susp of (unit -> 'a)

(* delay: (unit -> 'a) -> 'a susp *)
fun delay c = Susp c
(* forces computation of inner function *)
fun force (Susp c) = c ()

fun numsFrom n = Susp(fn () => Cons(n, numsFrom(n+1)))

fun smap f s =
  let
    fun mapStr (s) = mapStr'(force s)
    and mapStr'(Cons(x, s)) = delay(fn () => Cons((f x), mapStr(s)))
  in
    mapStr(s)
  end

6Exceptions¶

Cannot be polymorphic. Declare with exception NotFound of string; raise with raise NotFound "lol"; handle with handle NotFound "lol" => print "lol" | NotFound x => print "problem"

7Closures as objects¶

Done using partial evaluation/staging

Continuation: stack of functions. Can be used as function generators:

fun powG 0 = (fn n => 1)
  | powG k = let
      val cont = powG (k-1)
    in
      fn n => n * (cont n)
    end

(so powG 2 will generate a function that will square an input, etc)

Failure continuation: controls what to do when we have failed and need to keep going (e.g. in a find function in a binary tree, would keep track of what we still need to traverse in the tree)
Success continuation: controls what to do upon success (i.e. when we can return)

Usually: pass the identity function when initially calling it; will call all the functions that have built up on the way down (if necessary)

Staging to avoid having to do something more than once (from the notes on higher-order functions):

fun testCorrect x =
  let
    val z = horribleComp(x)
  in
    (fn y => z + y)
  end

Save the function returned by testCorrect and you can call it without having to call horribleComp again.

8References¶

! is a built-in function of type fn : 'a ref -> 'a. := is an infix operator, and not a built-in function.

9Proof by induction¶

Make sure to state properties used, e.g. associativity or commutativity or whatever of operators.

9.1Tail recursion proofs¶

Lemma: figure out where to put the acc on the non-tr side (there should only be one place that makes sense - e.g. acc @ (map f t) or (range (n-1)) @ acc or sum l + acc or (rev l) @ acc). Induction should be on the list l or the number or whatever (NOT the acc)

Base case: [] or 1 or 0 or whatever. Induction hypothesis: n-1 or t or whatever. Induction step: n or (h::t) or whatever. By the induction hypothesis, using whatever for the acc (and probably associativity/commutativity etc on the way), the two sides are equal so the lemma is true.

Then prove the main theorem, using [] or 0 or whatever for the acc.

10Environment diagrams¶

structured collection of frames, each of which is a box containing at most one name-variable binding pair etc and has a pointer to its enclosing environment

From assignment 5:

let
  val y = 1
  val x = 2
in
  let
    val f = let val x = y in fn u => (u + x + y) end
  in
    let val y = 4 in f(y) end
  end
end

10.1With references¶

From the end of the lecture notes:

let val x = 5
    val r = ref(10+x)
    val x = 1
    fun foo x = let val x = 10 in !r + x end
    val _ = (r := x+1)
in
    foo(x + !r)
end

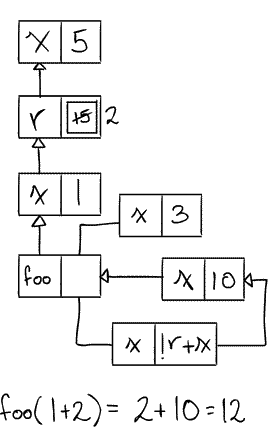
Although it should actually be an arrow to a separate box for the ref cell. Don't track the intermediate steps (or if you do, cross them out or something)

11Theoretical aspects¶

Type safety. If a program is well-typed, then every intermediate state during evaluation is defined and well-typed (so an expression has the same type as what it evaluates to - types are preserved). Progress means either it has a type or we can evaluate it further until it does, preservation means types are preserved etc

Types classify expressions according to their value. If we know what values there are in a language, we know what types there are.

Type annotations: useful when we cannot infer the type of something directly (e.g. fn x => x)

Value soundness: when everything evaluates to a value, happens when there are only bools and ints lol

Determinacy: each expression evaluates to only one value (same every time)

Principle type: a general type from which all others can be derived - $\alpha$!

11.1Free and bound variables¶

Free variables: variables that are not defined in the given context

e.g. in let val x = 5 in x + y end, y is not defined in the context, so it's free

Rules:

• FV(n) = {} where n is a number.
• FV(x) = {x} where x is a variable presumably
• FV(e1 op e2) = FV(e1) ∪ FV(e2)
• FV(let x = e1 in e2 end) = FV(e1) ∪ F(e2) \ {x}

11.1.1Substitution¶

Substitution syntax: [x/y]e means replace all instances of y with x (in e)

• [e/x] n = n
• [e/x] x = e
• [e/x] y = y
• [e/x] (e1 op e2) = [e/x] e1 op [e/x] e2
• [e/x] (let y=e1 in e2 end) =
let y = [e/x] e1 in [e/x] e2 end
  if y $\notin$ FV(e)

Must be capture-avoiding - rename ($\alpha$-conversion, change of bound variables)

11.2Type inference¶

Should be able to infer the type of something following the process given in class, although there's no need to memorise any specific type inference rules (they'll be given if necessary).

Hindley-Milner type inference: infer the most general type of an expression without type annotations. Requires unification (complicated to implement), does not scale to richer types

Unification: for solving constraints

11.3Type checking¶

e.g. for if/else expressions:

$$\frac{e_0 \Downarrow true \quad e_1 \Downarrow v}{if \,e_0\, then\, e_1\, else \,e_2 \,\Downarrow v}$$

11.3.1Bi-directional type checking¶

Check that the expression has the required type. Then synthesise the type for it.

11.4Subtyping¶

e.g. int is a subtype of real. Something that is an int is also a real. This is not true in SML, though it is true in general (which is almost the opposite of subtyping, I think). Upcasting (from int to real) is safe; downcasting is not generally safe. You can't provide a real whenever an int is required, though you can provide an int when a real is required since ints are reals etc etc

Products: covariant; records: more fields is a subtype of fewer fields (width subtyping instead of depth); functions: contravariant in input type, covariant in output type:

$$\frac{T_1 \leq S_1 \quad S_2 \leq T_2}{S_1 \rightarrow S_2 \leq T_1 \rightarrow T_2} \text{ (for functions)}$$

No subtyping on references - they are invariant.

11.5Overloading vs polymorphism¶

Overloading

same name, different method signature due to different arguments (Java)

Polymorphism

A function that can operate on input arguments of different types (e.g. fn x => x, fn x => (x, "lol"))

12Miscellaneous¶

Function application: left-associative (f g "test" equivalent to (f g) test)
Function types: right-associative (int -> int -> bool equivalent to int -> (int -> bool))

12.1Modules¶

Modules: two parts - signature and structure

Signature

interface of a structure

Structure

program consisting of declarations, can have more components than a signature, can have more general types (e.g. 'a instead of int), can use concrete datatypes without having to expose their workings through the signature`