These course notes are for COMP 302: Programming Languages and Paradigms, offered at McGill University in the Winter 2012 semester, taught by Professor Brigitte Pientka. These notes are simply an adaptation of what the instructor wrote on the board or mentioned in class, and may contain errors. These notes were originally written in LaTeX by Ryan Ordille (@remo), and were converted into Markdown and posted on Wikinotes with permission. No copyright infringement is intended.
These course notes can also be found, in PDF and .tex format, at https://github.com/ryanordille/c302w12.
- 1 09 January
- 2 11 January
- 3 13 Jan
- 4 16 January
- 5 18 & 20 January
- 6 23 January
- 7 25 & 30 January
- 8 03 February
- 9 6 February
- 10 8 February
- 11 10 February
- 12 13 February
- 13 15 February
- 14 27 February
- 15 02 March - Post-Midterm
- 16 05 March -- Post-Midterm Material
- 17 07 March
- 18 09 March
- 19 12 March
- 20 14 March
- 21 16 March
- 22 19 March
- 23 21 March
- 24 23 March
- 25 26 March
- 26 28 March
- 27 30 March
- 28 02 April
- 29 04 April
- 30 11 April
- 31 13 & 16 April
109 January¶
1.1Introduction to Functional Programming in Standard ML¶
1.1.1What are types?¶
Types classify terms (expressions) according to the properties of values.
4 : int ~1 : int 3+2 : int 5 div 2 : int 3.0 : real 3.0/4.2 : real 3.0 + 4.2 : real
Here, notice that + is an overloaded operator that works with both ints and reals. The division operator is not, however, so SML will make a distinction between div for integer division and / for real division.
We cannot mix types in SML, e.g. 3.2 + 1 will return a type error.
"abc" : string #"a" : character
Types are a static approximation of the run-time behaviour of the program -- type checking is done before execution.
If-statements must have a boolean as the guard, and two possible branches must be of the same type. However, the type checker is not "smart".
if true then 3.0 else 4.2 : real if false then 4 else 1 div 0 : int (* again, type checker is not smart *) if false then 1 else 2.0 (* type error - branches do not agree on a type *)
211 January¶
2.1Bindings and scope of variables and functions¶
val pi = 3.14
Binding: variable name paired with a value. Note that bindings are different than assignments found in imperative languages.
Local bindings:
let val m = 3 val n = m*m (* n=9 *) val k = m*m (* k=9 *) in k*n (* 81 *) end;
In the above example, m,n,k disappear after the end keyword. Notice that SML uses bindings, not assignments, so there exist some overshadowing issues to keep in mind:
val k = 4 let val k = 3 in k*k (* final value is 9, not 16 *) end k (* returns 4*)
2.2Functions¶
Functions in SML (and all functional languages, by definition) are values.
(* area : real -> real *) val area = fun r => pi * r * r (* or, equivalently and more compactly: *) fun area r = pi * r * r (* to explicitly restrict a type: *) fun sqr (x : real) = x * x (* using one parameter *) fun add (x : real, y : real) = x + y
Functions use the values of the most recent binding of the variables within themselves. For example:
val a2 = area (2.0) (* 12.56 *) val pi= 6.0 val a3 = area (2.0) (* still 12.56 *)
In order to update functions, you must re-declare the function to overshadow the previous binding.
The structure of the input of functions is important!
(* add : int -> int -> int *) add (x : int) (y : int) = x + y (* add' : (int * int) -> int *) add' (x : int, y : int) = x + y
The function add' takes in one argument -- a tuple with two elements -- whereas add takes in two separate arguments.
2.3Recursion in SML¶
exception Domain fun fact n = let fun fact' 0 = 1 | fact' n = n * fact' (n-1) in if n >= 0 then fact' n else raise Domain end
Note that the above method is nowhere near the most efficient way of expressing the factorial function, but it works as an example of recursion in this case.
313 Jan¶
3.1Data types¶
We can define our own datatypes using the datatype keyword:
datatype Suit = Hearts | Diamonds | Spades | Clubs (* dom : suit * suit -> bool, where spades > hearts > diamonds > clubs *) fun dom (Spades, _) = true | dom (_, Clubs) = true | dom (Hearts, Diamonds) = true | dom (S1, S2) = (S1 = S2)
SML will warn you if your pattern-matching does not cover all possible cases.
datatype rank = Ace | King | Queen | Jack | Ten | ... type card = rank * suit (* instead of declaring a tuple every time, we can use this "abbreviation" *) val c0 = (Queen, Hearts)
The above are examples of finite data types.
Mathematically, a hand can be either empty, or, if $C$ is a card and $H$ is a hand, Hand(C,H) (this is an example of a constructor).
datatype hand = Empty | Hand of Card * Hand val h0 = Empty val h1 = Hand (c0, h0) val h2 = Hand ((King, Clubs), h1) (* count : hand -> int *) fun count Empty = 0 | count (Hand (_, h)) = 1 + count h
What about infinite data types?
3.1.1Lists in SML¶
Lists are an example of an incredibly useful datatype found in SML's base language.
A list is either empty (nil) or, if $A$ is an element and $L$ is a list, Cons(A,L).
Note here that 'a (pronounced "alpha", for $\alpha$) is a type variable for all possible types. This allows us to create polymorphic data types.
datatype 'a list = Nil | Cons of 'a * 'a list val l1 = Cons (1, Nil) (* : int list *) val l2 = Cons (Queen, Nil) (* : rank list *)
Lists are already defined in SML with a convenient syntax:
nil (* empty list *) [] = nil _::_ (* infix/cons operator *) 1::nil, 1::2::3::[]
All elements of a list must be of the same type. You can get around this by defining a new data type with the option of storing multiple values, if need be.
416 January¶
4.1Datatypes continued¶
datatype 'a option = None | Some of 'a (* hd : 'a list -> 'a option *) fun hd (h::_) = Some h | hd [] = None (* naive append function *) (* app: ('a list * 'a list) -> 'a list *) fun app ([], l2) = l2 | app (h::t, l2) = h::(app (t,l2)) (* @ is the built-in append operator in SML *) (* rev : 'a list -> 'a list *) fun rev [] = [] | rev (h::t) = (rev t) @ [h] (* this is O(n^2) in time because of the append operator *) (* using tail-recursion in O(n) time*) fun rev_tl l = let fun rev ([], acc) = acc | rev (h::t, acc) = rev(t, h::acc) in rev (l,[]) end
A binary tree is either empty or, if L and R are binary trees and v is a value of type $\alpha$, Node(v,L,R).
datatype 'a tree = Empty | Node of 'a * 'a tree * 'a tree (* size : 'a tree -> int *) fun size Empty = 0 | size (Node(_, L, R)) = size L + size R + 1 (* insert: (int * 'a) -> (int * 'a) tree -> (int * 'a) tree *) fun insert e Empty = Node(e, Empty, Empty) | insert ((x,d) as e)(Node((y,d'),L,R)) = if x=y then Node(e,L,R) else if x<y then Node((y,d'), (insert e L), R) else Node((y,d'), L, (insert e R))
518 & 20 January¶
5.1Mathematical Induction¶
See induction pdf.
623 January¶
6.1Higher-Order Functions¶
Functions as values -- can pass to functions or return as results! This allows us to create modular, reusable code.
fun sumInts (a,b) = if a>b then 0 else a + sumInts (a+1,b) fun sumSqrs (a,b) = if a>b then 0 else (a*a) + sumSq (a+1,b) fun sumCubes (a,b) = if a>b then 0 else (a*a*a) + sumCubes (a+1,b) (* etc. *)
The above code is not very clean or reusable -- what if we wanted to sum the powers of 100? We want to abstract what we're doing.
(* sum : (int -> int) * int * int -> int *) sum (f,a,b) = if a > b then 0 else (f a) + (sum (f,a+1,b)) fun sq x = x*x fun sumSq (a,b) = sum (sq, a, b) fun id x = x fun sumInts (a,b) = sum (id, a, b)
It's a bit silly to give all these functions names, so we can define functions "on the fly" without giving them names:
fun sumInts (a,b) = sum ((fn x => x), a, b) val id = (fn x => x) fun sumSq (a,b) = sum ((fn x => x*x), a, b)
Our only real restriction on anonymous functions is that they cannot be recursive, since you need to give names to recursive functions to call them.
fun inc [] = Empty | inc (h::t) = (h+1)::(inc t) (* What if we wanted to multiply each element? Square each element? *) fun map f [] = [] | map f (h::t) = (f h)::(map f t) (* filter out all elements which are, say, even *) fun filterEven [] = Empty | filterEven (h::t) = if h mod 2 = 0 then h::filterEven t else filterEven t (* filter : ('a -> bool) -> 'a list -> 'a list *) fun filter f [] = [] | filter f (h::t) = if f h then h::filter t else filter t
725 & 30 January¶
These two lectures were taught by a TA, and cover higher-order functions, currying, and staging evaluation. The material can be found in the relevant pdfs.
Link to PDF: http://cs.mcgill.ca/~cs302/handouts/hofun.pdf
803 February¶
Continuations
8.1Regular Expression Matching¶
Typical patterns:
- Singleton: matching a specific character
- Alternation: choice between two patterns
- Concatenation: succession of patterns
- Iteration: repeat a certain pattern (indefinite)
Regular expressions;
- 0 and 1 are regular expressions.
- If $a \in \Sigma$ where $\Sigma$ is an alphabet, then $a$ is a regular expression.
- If $r_1$ and $r_2$ are regular expressions, then $r_1 + r_2$ (choice) and $r_{1}r_{2}$ (concatenation) are regular expressions.
- If r is a regular expression, then $r^*$ is a regular expression (repetition).
Examples;
a(p*)l(e+y)matches against "apple", "apply", "ale"g(1+r)(e+a)ymatches against "grey", "gray", "gey", "gay" (1means you can either have something there or not)g(1+o)*glematches "google", "ggle"
Our goal is to implement a regex matcher in SML.
Regular expression algorithm:
s matches 1 iff s is empty s matches a iff s = a s matches r1+r2 iff either s matches r1 or s matches r2 s matches r1r2 iff s = s1s2 and s1 matches r1 and s2 matches r2 s matches r* iff either s is empty or s = s1s2 where s1 matches r and s2 matches r*
Remember that continuations tell us what to do once an initial segment of the input char list has been matched.
In SML, using continuations:
datatype regexp = Zero | One | Char of char | Plus of regexp * regexp | Times of regexp*regexp | Star of regexp (* acc r s cont = bool *) (* acc: regexp -> char list -> (char list -> bool) -> bool *) (* ex: a(p*)l(e+y) on [a,p,p,l,e] *) fun acc (Char c) [] cont = false | acc (Char c) (c1::s) cont = c = c1 andalso (cont s) | acc (Times (r1,r2)) s cont = acc r1 s (fn s2 => acc r2 s2 cont) | acc (Plus (r1,r2) s cont = acc r1 s cont orelse acc r2 s cont | acc One s cont = cont s | acc (Star r) s cont = (* remove (1*) case - s must shrink *) (cont s) orelse acc r s (fn s' => not (s = s') orelse acc (Star r) s' cont)
96 February¶
9.1Exceptions¶
We use exceptions to quit out from the runtime stack. We have already seen some built-in exceptions - for example, SML will throw a Div exception if you try to divide by zero (like 3 div 0). Exceptions like this are used to abort a program safely whenever invalid input is given.
(* define the exception *) exception Error of String; fun fact n = let fun fact' n = if n = 0 then 1 else n * fact'(n-1) in if n < 0 then raise Error "Invalid Input" else fact' n end; (* non-exhaustive warning *) fun head (h::_) = h; (* uncaught exception Match *) head [];
Sometimes we want to handle exceptions:
(* runFact: int -> unit *) fun runFact n = let val r = fact n in print ("Factorial of " ^ Int.toString n ^ " is " ^ Int.toString r) end handle Error msg => print ("Error: " ^ msg)
To sequentialize expressions, use the ; operator. exp1;exp2 first executes exp1 then executes exp2. This is equivalent to (fn x => exp2) exp1. This will be expanded upon in the next lecture.
We can pattern match on error codes:
(* define the exception *) exception Error of int; fun fact n = let fun fact' n = if n = 0 then 1 else n * fact'(n-1) in if n < 0 then raise Error 00 else fact' n end; fun runFact n = let val r = fact n in print ("Factorial of " ^ Int.toString n ^ " is " ^ Int.toString r) end handle Error 00 => print ("invalid input") | Error 11 => print ("blah") | Error _ => print ("Something else")
Exceptions cannot be polymorphic, e.g. it cannot be of type 'a list but can be of type int list.
Exceptions are usually pretty powerful in managing runtime stacks, but usually continuations are more powerful.
(* first arg: list of coins, second: what we want to get change for *) change [50,25,10,5,2,1] 43; (* result: [25,10,5,2,1] *) exception Change (* change: int list -> int -> int list *) fun change _ 0 = [] | change [] amt = raise Change | change (coin::coins) amt = if coin > amt then change coins amt (*ignore this coin, look at other available coins*) else cont change (coin::coins) (amt - coin) (*could raise Change exception in following recursive steps *) handle Change => change coins amt
There are some situations where we cannot give change at all, but change does not handle these situations. Below, we handle this situation - change might not be able to do anything but raise Change, so this must be caught.
fun change_top coins amt = let val r = change coins amt in print ("Change:" ^ ListToString r) end handle Change => print "Sorry, can't give change."
change [5,2] 8 =>* if 5>8 then ... else (5::change[5,2] 3 handle Change change [2] 8) change [2] 3 =>* 2::(change [2] 1 handle Change change [] 1) change [2] 1 => change [] 1 => raise Change (* goes to handle Change change [] 1 *) (* then goes to handle Change change [2] 8, which succeeds *)
108 February¶
10.1References (State)¶
Recall the binding/scope rules from the beginning of the class:
let val pi = 3.14 val area = fn r => pi * r * r val a2 = area 2.0 (*a2 = 12.56 *) val pi = 6.0 in area (2.0) (* a2 = 12.56 *) end;
So far, we have only seen bindings like the one above. For bindings, remember we have a variable name bound to some value.
Today we will look at references, which are a form of mutable storage. References allow us to to imperative programming.
Commands:
- Initialize a cell in memory:
val r : int ref = ref 0whereris the name of the cell and0is the content of the cell
val s : int ref = ref 0wheresandrdo not point to the same cell in memory - Read what is stored in a cell:
val x = !rwill read from locationrthe value0
r : int refand!r : int - Write some value into a cell (i.e update the content):
r := 5 + 3wherer : int refand5+3 : int
Previous content of cellris erased when we store8.
Evaluatingr:=3returnsunitand as an effect updates the content of the cell with3.
val x = !s + !r binds x to 3.
val t = r essentially makes two names for the same cell in memory. Calling val y = !t binds y to the value of r. This is called aliasing.
We can rewrite our beginning function:
let val pi = ref 3.14 val area = fn r => !pi * r * r val a2 = area 2.0 (* a2 = 12.56 *) val _ = (pi := 6.0) in area (2.0) (* 24.00*) end
Now we can program mutable data structures like Linked Lists:
datatype 'a rlist = Empty | RCons of 'a * ('a rlist) ref; val l1 = ref (RCons(4, ref Empty));
For l1, we now have a value 4 with a reference to some place in memory with an Empty list.
val l2 = ref (RCons(5,l1));
For l2 we have a value 5 with a reference to l1 defined above.
l1 := !l2;
The above will remove the value of l1, change it to 5 (l2's value) and create a reference back to this element. Here, we've created a circular list.
type 'a reflist = ('a rlist) ref; (* rapp: 'a reflist * 'a reflist -> unit *) (* returns unit as all we're doing is updating space in memory *) fun rapp (r1 as ref Empty, r2) = r1 := !r2 | rapp (ref (RCons (x,t)), r2) = rapp (t, r2)
Now we can check this with some examples:
val rlist1 = ref (RCons(1,ref Empty)) val rlist2 = ref (RCons(2,ref Empty)) rapp (rlist1, rlist2)
1110 February¶
11.1References and the environment diagram¶
11.1.1References for modelling closures and objects¶
local val counter = ref 0 in (* tick: unit -> unit *) fun tick () = counter := !counter + 1 (* reset: unit -> unit *) fun reset () = counter := 0 (* read: unit -> int *) fun read () = !counter end
We can use this to create a counter program:
fun newCounter () = let val counter = ref 0 fun tick () = counter := !counter + 1 fun reset () = counter := 0 fun read () = !counter in {tick = tick; reset = reset; read = read} end val c1 = newCounter (); val c2 = newCounter (); #tick c1 (); (* increments c1's counter *) #tick c2 (); #tick c1 (); #read c1 (); (* returns 2 *) #read c2 (); (* returns 1 *)
In essence, we've created an object - every time we create a new counter, we create an instance of the object. We can now program in the object-oriented paradigm using ML (although the syntax isn't quite as built for OOP).
11.1.2The Environment Diagram¶
let val x = 5+3 in x+7 end: will replace x by 8 then compute 8+7.
So far, evaluation is driven by substitution. We substitute the value of x into the body. Unfortunately, the substitution model fails when we have references because substitutions cannot capture global effects.
We have three different kinds of bindings we'd like to track using the environment diagram. A binding is an association between a variable and a value.
val x = 3+2creates a "box" with the variable namexand its value5.val x = ref (8+2)creates a box with the variable name and a location pointing to another box with the value10.val f = fn x => x + 3creates a box with the function name and a location pointing to a box with the input and the function body, where this box points back to the original box.
val f = let val y = 8+2 in fn y => y + x endadds another box (an extra step) with the local body.
1213 February¶
12.1Lazy Evaluation¶
So far, we've had an eager evaluation strategy. For example, let x = e1 in e2 end will evaluate e1 to some value v1 and bind x to the value v1, then evaluate e2. This is also known as a call-by-value strategy. Why should we evaluate e1 if we never use it at all?
This is especially relevant with "harder" computations.
let val y = horribleComp(322) in 3*2 end
With the call-by-value strategy, we always compute horribleComp(322), even if we never use it.
We also have the call-by-name strategy. In the original example, it will bind x to the expression e1, then evaluate e2. However, if we use x multiple times in e2, we are evaluating e1 multiple times.
There's a "best of both worlds" strategy we can also use -- the call-by-need strategy. In our original example, the call-by-need strategy will bind x to the expression e1, then evaluate e2, but memorize the result of evaluating e1.
Lazy evaluation is not only useful for saving computation time, but it also useful for evaluating infinite data structures. A stream of numbers online or interactive input/output from users would not be possible to deal with without infinite data structures.
Remember that continuations delay computation within functions. We can wrap functions around things we wish to delay.
datatype 'a susp = Susp of (unit -> 'a) (* takes in a continuation and wraps it in a suspension to delay computation *) (* delay: (unit -> 'a) -> 'a susp *) fun delay c = Susp c (* forces computation of inner function *) fun force (Susp c) = c ()
Now we can use lazy evaluation with the horribleComp example:
(* original *) let val x = horribleComp(522) in x+x end (* call-by-name model *) let val x = Susp(fun () => horribleComp(522)) in force x + force x end (* call-by-need *) (* Not sure if this is correct *) val memo = ref None val x = Susp (fun () => case memo of None => let val y = horribleComp(522) in memo := y+y end | Some y => y (* infinite stream of 'a *) datatype 'a stream' = Cons of 'a * 'a stream withtype 'a stream = ('a stream') susp (* stream' shows the first element, hides the rest, while stream hides all *) (* create an infinite stream of, say, 1's *) fun ones () = Susp (fun () => Cons (1, ones ())) val o = ones() (* returns a Susp of a function *) (* take: int -> 'a stream -> 'a list take': int -> 'a stream' -> 'a list *) fun take 0 s = [] | take n s = take' n (force s) and take' 0 s' = [] | take' n (Cons(x,s)) = x::(take (n-1) s) val l = take 5 (ones ()) (*returns [1,1,1,1,1]*) (* numsFrom: int -> int stream *) fun numsFrom n = Susp(fn () => Cons(n, numsFrom (n-1)) take 5 (numsFrom 0); (* returns [0,1,2,3,4] *)
We can compute a stream of Fibonacci numbers:
val fibStream = let fun fib a b = Cons(a, Susp(fn () => fib b, (a+b))) in Susp(fn () => fib 0 1) end take 4 fibStream; (* [0,1,1,2] *)
1315 February¶
13.1Lazy programming continued¶
Recall from last class:
datatype 'a susp = Susp of (unit -> 'a) datatype 'a stream' = Cons of 'a * 'a stream withtype 'a stream = ('a stream') susp
Last class we saw how to create infinite streams of real numbers, natural numbers, etc..
(* shd: 'a stream -> 'a *) fun shd (Susp s) = shd' (s ()) (* shd': 'a stream' -> 'a *) and shd' (Cons (h,s)) = h
The first line is equivalent to fun shd s = shd' (force s).
(* ltail: 'a stream -> 'a stream *) fun ltail s = ltail' (* ltail': 'a stream' -> 'a stream *) and ltail' (Cons (h,s)) = s (* smap: ('a -> 'b) -> 'a stream -> 'b stream *) (* mapStr: 'a stream -> 'b stream *) (* mapStr': 'a stream' -> 'b stream *) fun smap f s = let fun mapStr s = mapStr' (force s) and mapStr' (Cons (x, xs)) = Cons(f x, Susp (fn () => mapStr xs)) in mapStr s end
(* addStreams: int stream * int stream -> int stream *) fun addStreams (s1, s2) = addStreams' (force s1, force s2) (* addStreams': int stream' * int stream' -> int stream *) and addStreams' (Cons (x,xs), Cons (y,ys)) = Susp(fn () => Cons(x+y, addStreams (xs,ys))) (* zipStreams: 'a stream * 'a stream -> 'a stream *) fun zipStreams (s1, s2) = zipStream' (force s1, s2) (* zipStreams': 'a stream' * ['a stream] -> 'a stream *) and zipStreams' (Cons (x,xs), s2) = Susp(fn () => Cons (x, zipStreams (s2, xs)))
We don't need to force both streams for the zipStreams function to save work.
(* filter: ('a->bool)*'a stream -> 'a stream *) fun filter (p, s) = filter' (p, force s) (* filter': ('a -> bool) * 'a stream' -> 'a stream *) and filter' (p, (Cons(x,xs))) = if p x then Susp(fn () => Cons (x, filter (p,xs))) else filter (p, xs)
1427 February¶
14.1Midterm Review¶
14.1.1Example 1: Proofs¶
fun sum [] = 0 | sum (h::t) = h + sum t fun sum_tl [] acc = acc | sum_tl (h::t) acc = sum_tl t (h + acc)
For the above code, we wish to prove that sum l = sum_tl l 0. We can do this using structural induction on l.
The base case is trivial. We'll start with the step case where l = h::t. Our induction hypothesis states that sum t = sum_tl t 0. We'll need to show that sum (h::t) = sum_tl (h::t) 0.
sum (h::t) => h + sum t sum_tl (h::t) 0 => sum_tl t (h+0) => sum_tl t h
This attempt will not work, since we want to use the IH. We'll need to generalize the theorem:
Lemma: For all lists t and for all accumulators acc, sum t + acc = sum_tl t acc is true. We'll also need to prove this using structural induction on t.
Base case: where t = []:
sum [] + acc => 0 + acc => acc sum_tl [] acc => acc
Both sides are equal, so our base case checks out.
Step case: where t = h::t':
IH: for all acc', sum t' + acc' = sum_tl t' acc' sum (h::t') + acc' => (h + sum t') + acc' [by program] =>* sum t' + (h + acc') [by associativity and commutativity] sum_tl (h::t') acc' => sum_tl t' (h + acc') [by program]
By the induction hypothesis using (h + acc) for acc', we know these are equal.
Now that we've proved the lemma, we need to prove the main theorem.
By the lemma, using l for t and 0 for acc:
sum l + 0 => sum l
14.1.2Example 2: Rewriting library functions¶
We have a library function:
tabulate f n returns [f0, f1, ..., fn]
We want to write this in a tail-recursive manner.
fun tabulate f 0 acc = (f 0)::acc | tabulate f n acc = tabulate f (n-1) ((f n)::acc)
Another example:
foldr f b [x1, ..., xn] returns f (x1, ..., f (xn, b))
Now, we want to write a list append function using foldr.
fun append l1 f2 = foldr (fn (x,r) => x::r) l2 l1
We can also write a filter function:
fun filter p l = foldr (fn (x,r) => if (p x) then x::r else r) [] l
(* all: ('a -> bool) -> 'a list -> bool *) fun all p [] = true | all p (h::t) = p h andalso all p t
1502 March - Post-Midterm¶
15.1Midterm review¶
15.1.1Question 1¶
Dot product of two vectors $a \dot b = \sum_{i=1}^n a_1 \times b_1$
Use pair_foldr $ = f(x_n,y_n,f(x_{n-1},y_{n-1}, \ldots, f(x_1, y_1, init)) \ldots )$.
(* pair_foldr ('a * 'b *'c -> 'c) -> 'c -> ('a list * 'b list) -> 'c *) fun prod_vect v w = pair_foldr (fn (a,b,c) => a*b + c) 0 (v, w)
15.1.2Question 2¶
Matrices question:
[ [ 1,3,-5], [2, 0, 4] ]
fun emptyMatrix B = all (fn l => l = []) B (* multiply a vector times a matrix *) fun sm (v, B) = if emptyMatrix B then [] else let val c = map (fn (x::xs) => x) B val B' = map (fn (x::xs) => xs) B in prod_vect (v,c)::sm(v,B') end
15.1.3Question 3¶
Proofs question: similar structure to past proofs
15.1.4Question 4¶
References question:
(* mon_ref: 'a -> (unit -> int) * (unit -> 'a) * ('a -> unit) *) fun mon_ref a = let val r = ref a val c = ref 0 in ( (fn () => !c), (fn () => (c := !c + 1; !r)), (fn a => (c := !c + 1; r := a) ) end
1605 March -- Post-Midterm Material¶
16.1Introduction to Language Design¶
"A good designer must rely on experience, on precise, logical thinking, and on pedantic exactness. No magic will do." -- N. Worth
Goal: a precise foundation for answering questions such as:
- How will a program execute?
- What is the meaning of a program?
- What are legal expressions?
e.g.fun foo x x = x+2andfoo 3 5returns 7 instead of 5 - What concept of a variable do we have?
- Where is a variable bound?
- When is an expression well-typed?
- Does every expression have a unique type?
- What exactly is an expression?
Code --> Parser (syntax checker) --> Type Checker (static semantics) --> Interpreter (operational semantics)
In this class, we'll go through the different stages of running an ML program -- parsing, type checking, and interpreting. To ensure a language will produce "correct" programs, we have to ensure that each of these stages produce correct results.
16.2Nano ML¶
We'll start with a small subset of ML.
Definition: the set of expressions is inductively defined as follows:
- A number is an expression.
- The boolean
trueandfalseare expressions. - If
e1ande2are expressions, thene1 op e2is an expression, whereop$\in \{$+,-,*,=,<$\}$. - If
e0,e1ande2are expressions, thenif e0 then e1 else e2is an expression.
A more compact way of defining expressions is the BNF grammar (Backus-Naur-Form):
Operator op := + | - | * | = | < | orelse Expression e := n | true | false | e1 op e2 | if e0 then e1 else e2 Value v := n | true | false
Examples of syntactically illegal expressions:
true false+35-
This does not type check, however -- for example, true + 3 is syntactically legal but ill-typed.
"An expression e evaluates to a value v" is equivalent to a judgement "e $\Downarrow$ v"
An expression if e0 then e1 else e2 evaluates to some value v if:
e0evaluates totrueande1evaluates tov.
This is equivalent to:
$$\frac{premise_1 \ldots premise_2}{conclusion}$$
For example:
$$\frac{e_0 \Downarrow true \quad e_1 \Downarrow v}{if \,e_0\, then\, e_1\, else \,e_2 \,\Downarrow v}$$
1707 March¶
17.1Language Design and Nano ML continued¶
Today we want to add variables and let expressions to our BNF grammar.
Expression e := n | true |false | ... | x | let x = e in e' end
x here represents a class of variables x,y,z,.... For example:
let z = if true then 2 else 43 in z + 123 end
The following examples are not well-formed:
let z = 302 in -z end let x = 3 in x let x =3 x+2 end
When is a variable bound? When is a variable free?
Free variables: variables that are not bound. FV(e) is the set of free variable names.
FV(n) = {}wherenis a number.FV(x) = {x}FV(e1 op e2) = FV(e1) ∪ FV(e2)FV(let x = e1 in e2 end) = FV(e1) ∪ F(e2) \ {x}
let x=5 in let y=x+2 in y+x end end
let x=x+2 in x+3 end
Bound variable names don't matter -- let y=x+2 in y+3 end.
17.2Substitution:¶
$$\frac{e \Downarrow v_0 \quad [v_0/x] e^{\prime} \Downarrow v}{let \, x = e \, in \, e^{\prime} \, end \Downarrow v}$$
To evaluate let x=e in e' end:
- Evaluate
etov0. - Substitute
v0forxine'. - Evaluate
[v0/x]e'tov.
Substitution: [e/x]e' = e'' -- in e', replace every free occurrence of x with e.
Examples:
[e/x] n = n[e/x] x = e[e/x] y = y[e/x] (e1 op e2) = [e/x] e1 op [e/x] e2[e/x] (let y=e1 in e2 end) =
let y = [e/x] e1 in [e/x] e2 end
ify$\notin$FV(e)
A problem: free variables in e may be bound y (captured) if we don't guarantee that the free variables of e and the bound variable y don't clash or overlap.
Renaming is a special case of substitution -- [y1/y] e = e'
Our substitution has to be capture-avoiding.
We can also add functions to our BNF grammar:
Expression e := ... | fn x => e
Evaluating functions: (fn x => e)
Functions are themselves values -- we can extend our values definition:
Values v := n | true | false | fn x => e
$$\frac{}{fn \, x => \, e \Downarrow fn \, x => \,e^{\prime}}$$
$$\frac{e_1 \Downarrow fn \, x => e \quad e_2 \Downarrow v_2 \quad [v_2/x] e \Downarrow v}{e_1e_2 \Downarrow v}$$
1809 March¶
- Evaluating expressions (recursion)
- Turning theory into code
- Modules
18.1Evaluation¶
In SML, you might write:
fun f (x) = if x=0 then 0 else x + f (x-1) (* equivalent to in Nano ML *) rec f => fn x => if x=0 then 0 else x + f (x-1) f 3 => if 3=0 then 0 else 3 + f (3-1) (* instead *) ( rec f => fn x => if x=0 then 0 else x + f (x-1) ) 3 (rec f => fn x => if x=0 then 0 else x + (rec f => fn x ....)) 3 => if 3=0 then 0 else 3 + (rec f => fn x ...) (3-1) => ... [e'/x] (fn y => e) = fn y => [e'/x] e provided y is not in FV(e') [e'/x] (rec f => e) = rec f => [e'/x] e where f is not in FV(e)
18.2Modules¶
ML: Core language and the Module Language
Modules: two parts -- signature and structure
Signature: interface of a structure
Structure: program consisting of declarations
When does a structure implement a signature?
:> makes the implementation of the structure opaque.
A structure can provide more components, but it cannot have fewer.
Structures may provide more general types (e.g. using 'a instead of int).
Structures may also implement concrete datatypes (e.g. in Queues, lists, etc.), but the signature keeps the type abstract. This is important for information hiding.
The order of declarations does not matter.
1912 March¶
19.1Types¶
Many ill-typed expressions will get "stuck". For example:
if 0 then 3 else 3+2 0+2 (* why is this ill-typed? *) (fn x => x+1) true
Our evaluator will accept these expressions, but typing should rule out these ill-formed expressions. These should lead to run-time errors. Typing will ensure that we never evaluate these expressions. There will be fewer run-time errors as a consequence.
Typing approximates what happens during run-time. Typing allows us to detect errors early and gives us precise error messages. As a consequence, programmers can spend more time developing and less time testing their programs.
When we type-check an expression, we prove the absence of certain program behaviours.
Safety: If a program is well-typed, then every intermediate state during evaluation is defined and well-typed.
Types classify expressions according to their value. If we know what values there are in a language, we know what types there are.
Recall Values v := n | true | false. So, for now:
Types T := int | bool
The shorthand e : T can be read as "expression e has type T".
Axioms:
n : intfalse : booltrue : bool
For if-expression if e then e1 else e2:
e : boole1 : Te2 : T
We need to check that e1 : T and e2 : T.
$$\frac{e_1 \,: \, int \quad e_2 \,:\,int}{e_1 + e_2 \,:\, int}$$
$$\frac{e_1 \,:\,T \quad e_2 \,:\,T}{e_1 = e_2 \,:\, bool}$$
We can add tuples to our expressions: Expressions e := ... | (e1, e2) | fst e | snd e. We can then add tuples to possible values:
Values v := n | false | true | (v1, v2) Types T := int | bool | T1 x T2
$$\frac{e_1 \,:\,T_1 \quad e_2 \, : \, T_2}{(e_1,\,e_2)\, :\, T_1 \times T_2}$$
Now for let-expressions:
let x=5 in x+3 end : int (* as 5:int and (assuming x : int) x+3 : int *)
Note that we need to reason about the type of variables.
$\Gamma \vdash e : T$ reads "Given assumption $\Gamma$, expression e has type T".
$$\frac{\Gamma \vdash e \,:\,bool \quad \Gamma \vdash e_1 \,:\,T \quad \Gamma \vdash e_2 \,:\,T}{\Gamma \vdash if\, e\, then \, e_1 \, else \, e2\, :\, T}$$
$$\frac{\Gamma(x) = T}{\Gamma \vdash x\,:\,T}$$
$$\frac{\Gamma \vdash e_1 \,:\,T_1 \quad \Gamma_1, x \,x:\,T_1 \vdash e_2 \,:\,T}{\Gamma \vdash let \, x = e_1 \, in \, e_2 \, end\,:\,T}$$
Context Gamma := | G1 x T
Each assumption is unique implies that each variable has a unique type! We'll come back to let expressions with assumptions later.
Axioms:
$$\frac{}{\Gamma \vdash n \, :\, int}$$
$$\frac{}{\Gamma \vdash false\, :\,bool}$$
$$\frac{}{\Gamma \vdash true \,: \,bool}$$
We can infer types:
G |- e : T + + -
Typing rules lend themselves to be interpreted as type-inference rules. They will infer a unique type.
2014 March¶
20.1Typing rules continued¶
When is an expression well-typed?
e := n | true | false | e1 op e1 | if e then e1 else e1 | (e1, e2) | x | let x=e in e' end T := int | bool | T1 x T2
e : T = "expression e has type T"
G |- e : T = typing assumption about variables (e.g. Given assumptions in T, expression e has type T)
$$\frac{\Gamma \vdash e \,:\,T^{\prime} \quad \Gamma \times T^{\prime} \vdash e^{\prime}\,:\,T}{\Gamma \vdash let \, x = e\, in \, e^{\prime} \, end\,:\,T}$$
Example:
$$\frac{\displaystyle \frac{}{\vdash 5\, :\, int} \quad \frac{\displaystyle\frac{}{x\,:\,int\vdash x\,:\,int}\quad \frac{}{x\,:\,int \vdash 3 \,:\,int}}{x\,:\,int \vdash x+3 \,:\,int}}{ \vdash let\, x=5 \,in\, x+3\, end}$$
For every expression, we can infer a type. Every expression has a unique type.
20.2Extensions¶
Today we will look at extensions -- functions, applications, recursion, and references.
T := ... | T1 -> T2 V := ... | fn x => e
assume x:int, verify that if x=0 else x+2 has type int ------------------------------------ fn x => if x=0 then 4 else x+2 : int
(* this rule cannot be interpreted as inferring a type *) G1xT1|-e:T2 ----------------------- G|-fn x => e : T1 -> T2 (* solution: annotate x with its type *) fn x : T1 => e fn x => if fst x=0 then snd x else 5 : int x int -> int
Without type annotations, fn x => x has infinitely many types. With type annotations, we can infer a unique type.
What is the most general type of an expression? 'a "principle type"
Extremely important rule:
G|-e1:T1->T2 G|-e2:T1 ------------------------- G |- e1 e2 : T2
New reference type:
T := ... | T1 ref | unit e := ... | !e | e := e' | ref e
G|-e : T ref ------------ G |- !e : T G|-e:T --------- G |- ref e : ref T G|-e:T ref G|-e':T ----------------- G |- e := e' : unit G1 f:T |- e : T -------------------------- G |- ref f => e : T (1) (2) sum: int->int, x:int |- sum(x-1)+x : int ----------------------------------------------------------------- sum int->int, x:int |- if x=0 then 0 else sum(x-1) + x : int ---------------------------------------------------------------- sum int->int |- fn x => if x=0 then 0 else sum(x-1) + x : int->int ---------------------------------------------------------------- rec sum => fn x => if x=0 then 0 else sum (x-1) + x : int -> int
2116 March¶
21.1Type inference and polymorphism¶
Can we infer a type for an expression?
Recall that we needed type annotations on functions. fn x : int => x
Does an expression have a unique type? fn x => x could have the type int->int or bool->bool, etc., however this function does have one principle type 'a->'a.
The question: how can we infer the principle type of an expression without being given type annotations?
Example:
double = fn f => fn x => f(f(x)) : ('a -> 'a) -> 'a -> 'a
Intuitively, we can now use this function in multiple ways.
double (fn x => x+2) 3 : int f ( f x ) ^ ^ ^ 'a->'b 'a->'b 'a 'b
Because of this contradiction, we cannot pass a $\beta$ to a function which expects an $\alpha$.
double (fn x => x) false : bool
Crucial in this: type variables
T := int | bool | T1 x T2 | T1 -> T2 | 'a
How do we instantiate type variables? Substitution!
[T/'a] (int) = int [T/'a] ('a) = T [T/'a] ('b) = 'b (where 'b != 'a) [T/'a] (T1 -> T2) = [T/'a] T1 -> [T/'a] T2
Two views:
- Are all substitution instances of
ewell-typed?
If e has some type T and constrains some type variables $\alpha_1, \ldots, \alpha_n$, then e has type[T1/'a1 ... Tn/'an] Tfor every $T_1, \ldots T_n$? - Does there exist some substitution instance such that e has type T?
For example: fn x => x+1 has type $\beta$? Choose for $\beta =$ int->int.
fn x => x has type $\beta$? Choose for $\beta=$int->int or bool->bool or, most generally, 'a->'a.
Will fn x => x+1 have type 'b->bool? No. there is no instantiation for 'b.
21.1.1Type inference¶
(1) use typing rules to generate constraints. <-- will always succeed
(2) solve constraints. <-- will sometimes fail
What is a constraint? For example, T=bool.
Constraint C := T=T' | tt | C1 ^ C2
How do we collect constraints? Informally, to infer a type for if e then e1 else e2, we do the following:
- Infer a type $T$ for $e$ (and $C$).
- Infer a type $T_1$ for $e_1$ (and $C_1$).
- Infer a type $T_2$ for $e_2$ (and $C_2$).
Constraints: T = bool ^ T1 = T2.
To infer a type for fn x => e:
- Assume $x$ has type $\alpha_1$.
- Infer a type $T_24$ (provided the constraints $C$ can be solved).
- We then know that
fn x => ehas type'a1 -> T2(provided the constraints $C$).
\G |- e => T Cmeans "given the assumptions $\Gamma$ for an expression $e$, the type $T$, and the constraints $C$", or "the expression $e$ has type $T$ provided I can solve $C$".
21.1.2Solving constraints¶
G |- e => T/C G |- e1 => T1/C1 G |- e2 => T2/C2 ---------------------------------------------------- G |- if e then e1 else e2 => T2 / T=book ^ T1=t2 ^ C ^ C1 ^ C2 G1 x:'a1 |- e => T2/C ------------------------- G |- fn x => e => a1 -> T2 / C input: left of => output: right of => x:'a1 means 'a1 is new fn x => if 3=1 then 55 else x : 'a1 -> assuming x:'a1 constraint: int = 'a1 ^ bool=bool
Solving the constraints, we learn that 'a1 = int, and therefore
fn x => if 3=1 then 55 else x : int->int
------------------ G |- n => int / tt ---------------------- G |- true => bool / tt G(x) = T ---------------- G |- x => T / tt
2219 March¶
Some small mistakes on HW4 -- see WebCT for more details.
22.1Type inference¶
Examples:
fn f => fn x => f (x) + 1 : 'a1 -> 'a2 -> int f: 'a1, x: 'a2 |- f(x) + 1 : int f(x) : int 'a1 = 'a2 -> int .: the type of the fn is ('a2->int) -> 'a2 -> int as f : 'a2->int
A slightly more complicated example:
fn f => fn g => fn x => f( g x) + g x : 'a1 -> 'a2 -> 'a3 -> int f: 'a1, g: 'a2, x: 'a3 |- f(g(x)) + g(x) : int Constraints to solve: 'a2 = 'a3 -> int (from last g(x)) 'a2 = 'a3 -> 'a4 (from first g(x)) 'a1 = 'a4 -> int 'a2 = 'a3 -> 'a4, 'a2 = 'a3 -> int (intuitively) 'a1 = 'a4 -> int .: 'a4 = int, 'a1 = int -> int No constraint on 'a3 .: the type we infer is: (int -> int) -> ('a3->int) -> 'a3 -> int f g x
Third example:
fn f => fn x => f x + x f f: 'a1, x: 'a2 |- f x + x f 'a1 = 'a2 -> int 'a2 = 'a1 -> int 'a1 = ('a1 -> int) -> int Does there exist an instantiation for 'a1 such that 'a1 = ('a1 -> int) -> int ? There is no solution to make both sides equal. Reason: variable on the LHS occurs embedded on the RHS (circular).
22.2Unification Algorithm¶
Input: set of constraints
Question: Does there exist an instantiation such that all constraints are true?
C := tt | C1 ^ C2 | T = T'
C =====> C' until we reach our goal where C =>* tt.
C ^ tt => C C ^ int = int => C C ^ bool = bool => C C ^ T1->T2 = S1->S2 => C ^ T1=S2 ^ T2=S2 C ^ 'a = T => [T/'a] C (provided 'a is not in FV(T)) (occurs check -- prevents circular terms) C ^ T = 'a => [T/'a] C (same provisions)
unify (T1, T2) = (* pattern match on T1, T2 *) (* return bool *)
22.3Examples (part 2)¶
double = fn f => fn x => f (f x) : 'a1 -> 'a2 -> 'a3 f:'a1, x:'a2 |- f (fx) : 'a3 inter (f x) ---> 'a1 = 'a2 -> 'a4 outer f (f x) -> 'a1 = 'a4 -> 'a3 'a4 -> 'a3 => 'a2 -> 'a1 'a4 = 'a2, 'a3 = 'a4 .: 'a2 = 'a3 = 'a4 .: we infer: ('a2 -> 'a2) -> 'a2 -> 'a2 double (fn x => x+1) 5; double (fn x => x) true; let d = fn f => fn x => f (f x) x = d (fn x => x+1) 5 y = d (fn x => x ) true in (y, x) end (* this will type-check in SML, but would not type check in our definition so far, * as we don't have a way to reuse a function with different types as we've * given it a type. SML will abstract over polymorphic type variables, i.e. * it can reuse the type over multiple types by saying "for all 'a2:('a2->'a2)->'a2->'a" *)
2321 March¶
23.1Type inference continued¶
23.1.1Warm-up examples¶
Example 1:
fn f => fn g => fn x => if gx then f(g x) else f(f(g x)) f : 'a1, g : 'a2, x : 'a3 |- if (g x) then f(g x) else f(f(g x)) : 'a4 'a1 -> 'a2 -> 'a3 -> 'a4
We are looking for instantiations for 'a1, 'a2, 'a3, 'a4 such that the expression is well-typed.
(g x) == 'a2 = 'a3 -> bool f(g x) == 'a1 = bool -> 'a4 f(f(g x)) == 'a1 = 'a4 -> 'a4 .: 'a4 = bool
This given function will have type (bool->bool)->('a3->bool)->'a3->bool.
Example 2:
fn f => if f true then f 5 else f 4 f:'a1 |- if f true then f 5 else f 4 : 'a2 f true == 'a1 = bool -> bool f 5, f 4 == 'a1 = int -> 'a2 bool->bool != int -> 'a2 (* won't type check? *) (* in SML *) let val f = fn x => x in if (f true) then (f 5) else (f 4) end (* will type int -- why? *)
In our algorithm:
f : 'a -> 'a |- if (f true) then f 5 else f 4 (f true) == 'a -> 'a = bool -> bool f 4 == 'a -> 'a = int -> int f 5 == "" 'a = int 'a = bool
Our algorithm does not do what SML does -- it cannot truly reuse f in multiple ways.
To make this function type check in our language, we'll need different copies of f.
Observation: if (fn x => x) true then (fn x => x) 5 then (fn x => x) 4 will type check -- each "sub-function" will be assigned its own relevant type. By writing this function three times, we will type check it three times, however we will have no constraints to carry over, so our language will type check this correctly.
23.1.2Modifying our typing rules¶
As a solution to this problem, we can modify our old rule, which is not suitable to handle polymorphic functions. Our new rule is as follows:
G|-[e1/x]e2 : T ----------------------- G |- let x=e1 in e2 : T
Note: type checks $e_1$ multiple times -- not very efficient, but at least this will work for polymorphism. In practical languages, this is not what happens. Instead, we'll need to make the assumption $\forall \alpha -> \alpha$, so whenever we look up the type of f, we get a "fresh", unique copy of its type.
In ML:
(generalize -- abstract over the free variables and quantify over them, so we can reuse them as often as we'd like)
G|- e1 : S G1 x generalize(S) |- e2 : T ----------------------------------------- G |- let x=e1 in e2 : T
In example 2, (forall 'a, 'a -> 'a) -> int -- full polymorphism. In ML, we have parametric polymorphism, where all quantification over type variables is at the outside. Some languages are slowly moving towards allowing full polymorphism.
23.1.3More examples¶
let val r = ref (fn x => x) in r := (fn x => x+1); !r true end
In SML, this will not type check; however, from the rules we have, it will.
ref (fn x => x) == ('a -> 'a) ref ref (fn x => x) := (fn x => x+1); (ref (fn x => x))! true 'a = int then 'a = bool "happy" but WRONG
In general, we can reuse functions and values in a polymorphic way, but we cannot make any general polymorphic assumptions about expressions which are not values! Recall that references are not values, so we cannot make any general polymorphic assumptions about references.
This is called value restriction -- we can only reuse values in a polymorphic way. If something is not a value, we cannot make any polymorphic assumptions about it, since there can be side effects and such.
let val r = ref (fn x => x) in r end (* SML *) Warning : type variables are not generalized because of value restriction are instantiated with dummy types: ?X1->?X1 ref
2423 March¶
HW 5 out -- due 11 April, 2012
24.1Bi-directional type checking¶
So far, we have type inference rules.
Hindley-Milner (type inference) -- Goal: infer the most general type of an expression without declaring any types, i.e., without type annotations.
Advantages of writing type annotations:
- Gives better error messages (programmer communicates his or her intent)
- High-grade (high-quality) documentation -- does not get out of sync with the code
- I can refuse types to force programs to be used in a specific way
- Hindley-Milner type inference does not scale to richer types such as sub-typing, full polymorphism, and dependent types.
- Hindley-Milner type inference is complicated and difficult to implement (unification is needed).
Basic idea behind bi-directional type checking -- instead of inferring a type:
$$\Gamma \vdash e \Rightarrow \tau$$
$\forall e$ where $\tau$ is the output, we'll use two judgements (functions), "check" and "synthesize". First, check $\Gamma \vdash e \Leftarrow \tau$ for inputs $\Gamma, e, \tau$ (check that expression $e$ has type $\tau$ under the assumptions $\Gamma$). Then, synthesize $\Gamma \vdash e \Rightarrow \tau$ (synthesize a type $\tau$ for expression $e$ under the assumptions $\Gamma$ for some $e$). Synthesize basically means infer.
This algorithm is based on two observations. First, we can't use information that we don't have. Second, we should try to use information that we do have.
Type variables:
$$\frac{}{\Gamma_i x \,:\, \tau \vdash x \Rightarrow \tau}$$
Functions
$$ \frac{\tau_i x \,:\, \tau_1 \vdash e \Leftarrow \tau_2}{\Gamma \vdash \text{fn x => e} \Rightarrow \tau_1 \rightarrow \tau_2}$$
$$\frac{\Gamma \vdash e_1 \Rightarrow \tau_2 \rightarrow \tau \quad \Gamma \vdash e_2 \Leftarrow \tau_2}{\Gamma \vdash e_1 e_2}$$
Example:
twice: (int -> int) -> int -> int) |- (twice (fn x => x+1)) 3 ---- ^ infer type (int->int)->int->int .: int
Conversion:
$$\frac{\Gamma \vdash e \Rightarrow \tau^{\prime} \quad \tau^{\prime} = \tau}{\Gamma \vdash e \Leftarrow \tau}$$
Example:
$$\frac{\vdash 3 \Rightarrow int \quad int = int}{\vdash 3 \Leftarrow int}$$
2526 March¶
25.1Subtyping¶
fun area r = 3.14 * r * r area : real -> real area 2 (* type error *)
We want to pass an int whenever a real is required (int $\leq$ real)
Subtyping principle: S $<$ T. S is a subtype of T if we can provide a value of type S whenever a value of T is required.
$$\frac{\Gamma \vdash e : S \quad S \leq T}{\Gamma \vdash e : T}$$
$$\frac{T \leq R \quad R \leq S}{T \leq S}$$
$$\frac{T_1 \leq S_1 \quad T_2 \leq S_2}{T_1 \times T_2 \leq S_1 \times S_2} \text{ (covariant)}$$
Records are a generalization of tuples (n-ary tuples where each element has a label).
$$\frac{\forall i \; T_i \leq s_1}{\{x_1 : T_1, \dots, x_n : T_1 \} \leq \{ x_1 : S_1, \dots, x_n : S_1 \} } \text{ (depth \; subtyping)}$$
Two things we want for records:
- Permutations of elements should be allowed!
$$\frac{\{ x_1 : T_1, \dots, x_n : T_n\} \leq \{ x_{\phi(1)} : T_{\phi(1)}, \dots, x_{\phi(n)} : T_{\phi(n)} \} }{ \phi \text{is a permutation}}$$
(MISSED FROM FAR BOARD lol)
$$\frac{\{x_1 : T_1, \dots, x_k : T_k\} < \{x_1 : T_1, \dots, x_n : T_n\}}{k > n}$$
25.1.1Function example¶
let (* areaSqr: real -> real *) fun areaSqr (r : real) = r*r (* areaFake: real -> int *) fun areaFake (r : real) = 3 in areaSqr 2.2 + 3.2 end
Question: Can we provide areaFake: real -> int whenever areaSqr: real -> real is required? YES, but not in SML -- our discussion of subtyping is purely theoretical.
Therefore,
$$\frac{T_2 \leq S_2}{T \rightarrow T_2 \leq T \rightarrow S_2}$$
2628 March¶
26.1Subtyping continued¶
26.1.1Review¶
Basic subtyping principle: $S \leq T$ "S is a subtype of T" if we can provide a value of type S whenever a value of type T is required.
Products: covariant int * real <= real * real real * int <= real * real
Functions: contravariant int -> int <= int -> real as int <= real and functions are co-variant in the output type.
real -> int <= int -> int as int <= real and functions are contra-variant in the input type.
Invalid: int -> int !<= real -> real
$$\frac{S_1 \leq T_1 \quad T_2 \leq S_2}{T_1 \rightarrow T_2 \leq S_1 \rightarrow S_2}$$
26.1.2References¶
let val x = ref 2.0 val y = ref 3 in !x + 3.14 end
This is a perfectly valid program, as x : real ref and y : int ref. Can we supply an int ref (e.g. y) whenever a real ref is required? YES (but, again, not in SML).
$$\frac{ S \leq T }{S ref \leq T ref}$$
let val x = ref 2.0 val y = ref 2 in y := 4 end
Should we be able to supply a real ref (e.g. x) whenever an int ref is required? YES. This seems almost contradictory, since we said yes to the previous question. The following rule seems incompatible to the one before:
$$\frac{T \leq S}{S ref \leq T ref}$$
Therefore, there is no subtyping on references (locations) -- references are invariant.
$$\frac{S \leq T \quad T \leq S}{S ref \leq T ref}$$
Of course, if $S \leq T$ and $T \leq S$, then $S = T$.
26.1.3More subtyping¶
Recall the typing rule for subtyping:
$$\frac{\Gamma \vdash e : S \quad S \leq T}{\Gamma \vdash e : T}$$
Upcasting is always safe with type annotations -- it is safe to "forget"!
$$\frac{\Gamma \vdash e : S \quad S \leq T}{\Gamma \vdash (T) e : T} \text{ (Upcasting)}$$
Below, there can be no relationship between S and T. This is not really safe in general. Most often, S is a supertype of T. You must trust that this is safe in order to use it.
$$\frac{\Gamma \vdash e : S}{\Gamma \vdash (T) e : T}$$
E.g. fn (x:real) => (int) x + 1 downcasts x to an int.
2730 March¶
27.1Dependent types¶
fun append [] l = l | append (h::t) l = h::(append t l) (* append: 'a list -> 'a list -> 'a list *)
What else do we know?
length (append l1 l2) = length l1 + length l2
How can types track information about the length of lists? Index a type by an object/expression which stands for an integer.
for all n : int, for all m : int: list 'a n -> list 'a m -> list 'a (plus n m)
Agda (a dependently typed functional language), DML (Dependent ML), Omega, Epigram, Coq, ...
Staring with simple types in Agda:
data Nat : Set where zero : Nat succ : Nat -> Nat data Bool : Set where true : Bool false : Bool data List (A : Set) : Set where [] : List A _::_ : A -> List A -> List A
In Agda, we have to explicitly declare the type of a program:
plus : Nat -> Nat -> Nat plus zero m = m plus (succ n) m = succ (plus n m) rev_tl : {A : Set} -> List A -> List A -> List A rev_tl [] acc = acc rev_tl (h::t) acc = rev_tl t (h::acc)
The {A : Set} clause is read as "for all A".
Dependent types:
Index a boolean list with its length
data BoolList : Nat -> Set where nil : BoolList zero cons : {n : Nat} -> Bool -> BoolList n -> BoolList (succ n) append : {n : Nat} -> {m : Nat} -> BoolList n -> BoolList m -> BoolList (plus n m) append nil l = l append (cons h t) l = cons h (append t l)
Surprisingly, the program didn't change at all! However, the type checker in Agda will do a lot more work for you than it did in SML, as our type declaration is much, much richer in our Agda code.
Type checker's tasks:
(1) l : BoolList m |- l : BoolList (plus n m)
We need to prove that BoolList m = BoolList (plus zero m). Show that plus zero m => m.
To check that two types are equal means we need to show that the index arguments are equal. This is based on evaluation!
$$ \frac{BoolList m = BoolList m'}{ m \Rightarrow m^{\prime}}$$
Agda works with total functions only -- i.e. those that are defined to work with all possible inputs. This way, the functions are provably terminating.
2802 April¶
28.1Dependent Types continued¶
cons: {n : Nat} -> Bool -> BoolList n -> BoolList (succ n)
For our append method (from Friday), consider the base case to be case 1 and the induction case to be step 2. To check case 1, can we show that BoolList m = BoolList (plus zero m)? BoolList m is the inferred type for l and the RHS is the expected type. Because plus zero m => m, we know that the two types are equal.
For case 2, we know cons h t : BoolList (succ n'), and therefore t : BoolList n'. append t l : BoolList (plus n' m), so cons h (append t l) : BoolList (succ (plus n' m)).
Expected type: BoolList (plus (succ n') m), because plus (succ n') m => suc (plus n' m), so we know that the two types are equal.
Vectors: polymorphic lists
data Vec (A : Set) : Nat -> Set where [] : Vec A zero _::_ : {n : Nat} -> A -> Vec A n -> Vec A (succ n) -- by using (succ n), we're prevented from ever getting a list of length zero vhead : {A : Set} -> {n : Nat} -> Vec A (succ n) -> A vhead h::t = h
Note that there is no case necessary for the empty list, so this vhead function is total.
vtail : {A : Set} -> {n : Nat} -> Vec A (succ n) -> Vec A n vtail h::t = t vmap : {A : Set} -> {B : set} -> {n : Nat} -> (A -> B) -> Vec A n -> Vec B n vmap f [] = [] vmap f (h :: t) = (f h)::(vmap f t) vzip : {A : Set} -> {B : Set} -> {n : Nat} -> Vec A n -> Vec B n -> Vec (A * B) n vzip [] [] = [] vzip (x::xs) (y::xs) = (x,y)::(vzip xs ys)
We'd also like to have a safe look-up function of the $k$th element in a vector:
data _ <= _ : Nat -> Nat -> Set where leq_zero : {n : Nat} -> zero <= n leq_succ : {n m : Nat} -> n <= m -> succ n <= succ m kth : {A : Set} -> {n : Nat} -> {k : Nat} -> k <= n -> Vec A (succ n) -> a kth zero leq_zero (x::xs) = x kth (succ k) (leq_succ p) (x::xs) = kth k p xs
2904 April¶
29.1Type-Preserving Evaluator with Agda¶
The type-preserving evaluator also guarantees that only values are returned.
Expressions e := true | false | zero | suc e | pred e | isZero e | switch e e1 e2 Values v := true | false | zero | suc v Types T := Bool | Nat
Well-typed expressions:
$$\frac{zero:Nat}{}$$
$$\frac{suc e : Nat}{e : Nat}$$
$$\frac{true : Bool}{}$$
$$\frac{false : Bool}{}$$
$$\frac{pred e : Nat}{e : Nat}$$
$$\frac{isZero e : Bool}{e : Nat}$$
$$\frac{switch e e1 e2 : T}{e : Bool& e1 :T&e1:T}$$
data tm : Tp -> Set where true : Tm Bool false : Tm Bool zero : Tm Nat suc : Tm Nat -> Tm Nat pred : Tm Nat -> Tm Nat isZero : Tm Nat -> Tm Bool switch : {t : Tp} -> Tm Bool -> Tm t -> Tm t -> Tm t data Tp : Set where Bool : Tp Nat : Tp
With these data definitions, suc true and switch zero true false will be ill-typed in Agda!
Defining values:
data Value : Tp -> Set where vtrue : Value Bool vfalse : Value Bool vzero : Value Nat vsuc : Value Nat -> Value Nat
Types are preserved during evaluation -- type safety.
eval : {t : Tp} -> Tm t -> Value t eval true = vtrue eval false = vfalse eval zero = vzero eval (suc e) = vsuc (eval e) eval (pred e) with eval e ... | vzero = vzero ... | vsuc _ = v
Note: these are the only possible two cases, since eval e produces a value of type Tm Nat because e has type Nat.
-- ... eval (iszero e) with eval e ...| vzero = vtrue ...| vsuc v = vfalse eval (switch e e1 e2) with eval e ...| vtrue = eval e1 ...| vfalse = eval e2
Agda enforces whitespace, similar to Python. Comments are prefaced by --. Within the Emacs environment, Agda has incremental type checking -- see documentation for details. In-class examples also include the pair/tuple term, the cross type, and the fst and scd functions with all the relevant evaluation functions.
3011 April¶
30.1Object-Oriented vs Functional¶
30.1.1Classes and types¶
In a language like Java:
Class A { ... } ^ | methods, fields Class B extends A { ... }
To say that B extends A, two things happen at the same time: inheritance (single inheritance only in Java) and subtyping.
Class B can add more methods and fields and/or overwrite methods. The same method exists in A and in B and it has the same types.
Example:
class myInt { private int n; /* ... */ public myInt add (myInt N){ /* ... */ } public void show () { /* ... */ } } class gaussInt extends myInt { private int m; // imaginary part /* ... */ // overloading example public gaussInt add (gaussInt z){ /* ... */ } // overwriting example public void show () { /* ... */ } }
The B extends A construct is an example of nominal subtyping.
There is no multiple inheritance in Java, but there is multiple subtyping.
Overloading -- same method name, different input types.
Typechecking needs to OK all method calls before running. All typechecking happens on the declared type. Subtyping is an integral part. Method lookup is based on the actual type of an object. Overloading is resolved by typechecking during runtime.
myInt a = new myInt (3); gaussInt z = new gaussInt (3, 4); myInt b = z; // OK because gaussInt <= myInt System.out.println("The value of z is " + z.show()); // OK System.out.println("The value of b is " + b.show()); // uses show from gaussInt int x = z.realPart (); // fine, so long as gaussInt has this method int y = b.realPart (); // typechecking will say no, although, during run time, we know that b is actually // a gaussInt myInt d = b.add(b); // chooses during runtime the method add from myInt gaussInt w = z.add(b);
Functionality = functions via pattern matching. All the functionality is in one place.
In SML:
datatype persons = | Doctor of string | Nurse of string | Patient of string fun display (Nurse s) = ... | display (Doctor d) = ... | display (Patient p) = ...
In Java:
Class Doctors extends personnel { /* ... */ } Class Nurses extends personnel { /* ... */ }
In Java, functionality scattered. This isn't necessarily bad, depending on what you want to do, but there are different consequences.
In functional languages, it's easy to add new functionality to functions, but harder to add new persons. In OO languages, it's hard to add new functionality to methods, but it's much easier to add a new class of people. There are many trade-offs you have to take into consideration.
3113 & 16 April¶
The lecture notes for these last two classes were compiled and posted by @ejanco.
31.1Induction Proof Example¶
fun size (Leaf) = 0 | size (Node(root, L, R)) = root + size L + size R fun size_tl (Leaf, acc) = acc | size_tl(Node(root, L, R), acc) = size_tl(L, size_tl(R, root + acc))
To prove: size T = size_tl (T, 0)
case T = Node(root, L, R)
IH1 size L = size_tl(L,0)
IH2 size R = size_tl(R,0)
Does not work :(
Instead,
Use lemma, choosing acc=0
Lemma: size T + acc = size_tl(T, acc)
By induction on T,
Base Case: T = Leaf
size Leaf + acc => 0 + acc => acc
size_tl(Leaf, acc) => acc
Therefore, these two sides are equal.
Step Case: T = Node(root, L, R)
IH1: For all accumulators:
size L + acc_L = size_tl(L, acc_L)
IH2: For all accumulators:
size R + acc_R = size_tl(R, acc_R)size_tl(Node(root, L, R), acc)
=> size_tl(L, size_tl(R, root+acc))By IH2, using root+acc = acc_R
=> size_tl(L, size R + (root + acc))
By IH1, using acc = size R + (root + acc)
=> size L + (size R + (root+acc))By assoc + comm
= root + size L + size R + accsize(Node(root,L,R)) + acc
=> root + size L + size R + acc
They're the same!, QED
31.2Backtracking¶
31.2.1With Exceptions¶
datatype 'a tree = Empty | Node of 'a tree * 'a * 'a tree exception FoundSoFar of int list (* Exception are not polymorphic - We NEED to use int *)
Task: Find all elements which satisfy a given predicate p
fun findAll'(p, Empty) = raise FoundSoFar [] | findAll'(p, Node(L, d, R)) = findAll'(p, L) handle FoundSoFar ll => (findAll'(p,R) handle FoundSoFar lr => if (p d) then raise FoundSoFar (ll@[d]@lr) else raise FoundSoFar (ll@lr)) fun findAll(p, T) = (findAll'(p, T) handle FoundSoFar l => l)
31.2.2With continuations¶
fun findAllCont' p Empty cont = cont [] | findAllCont' p (Node(L,d,R)) cont = findAllCont' p L (fn ll => findAllCont' p R (fn lr => if p(d) then cont (ll@[d]@lr) else cont (ll@lr))) (* Notice the similarities with the exceptions *) fun findAllCont p T = findAllCont' p T (fn l => l)
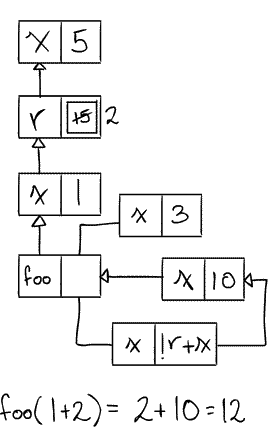
31.3Environment Diagram¶
let val x = 5 val r = ref(10+x) val x = 1 fun foo x = let val x = 10 in !r + x end val _ = (r := x+1) in foo(x + !r) end