Monday, December 2, 2013

Static dataflow

1Message passing¶

We have been using shared memory as our main paradigm for doing concurrent programming. However, we could have used processes and communication channels. This is the basic idea behind message passing.

There are two main branches.

Asynchronous message passing

Like snail mail

receiver blocks until the message arrives.

sender does not wait. The send operation immediately returns.

Variations: Bounded capacity channel, Message ordering (FIFO?), Reliability (100%?)

Synchronous message passing

Like a telephone call

receiver blocks as with asynchronous

sender does not return until the receiver receives the message

1.1Java example¶

Message passing is actually easy to implement in a language like Java.

public class SyncChannel {
  private Object msg;

  public synchronized void send(Object o) {
    msg = o;
    notify();
    while(msg != null) {
      wait();  // not needed for async
    }
  }

  public synchronized Object receive() {
    while(msg == null)
      wait();
    Object ret = msg;
    msg = null; // Indicate it has been consumed
    notfy();  // not needed for async
    return ret;
  }
}

public class AsyncChannel {
  // Left as an exercise
}

1.2Synchronous vs asynchronous¶

There are tradeoffs for both synchronous vs asynchronous. However, in a more theoretical sense, synchronous is better because it allows more flexibility in the design.

Consider the following example:

// Process P
send(Q, 23);

// Process Q
x = 0;
x = receive(P);

What does P know about Q?

In asynchronous, P does not know whether Q received the message or not. x == 0 | x == 23.

In synchronous, it knows that Q.x == 23 after send. More knowledge!

1.3Common knowledge¶

In asynchronous, when A sens a message m to B, the only way for A to know if B received m, is to receive back an acknowledgement. Yet, B does not know if A received the acknowledgement either.

We cannot gain common knowledge with asynchronous, but is implied with synchronous.

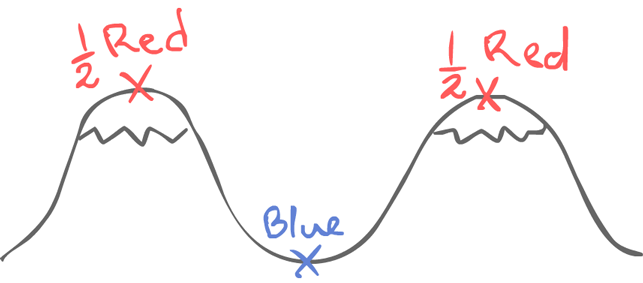
1.3.1The 2-army Problem¶

Jim Gray, 1978

If both red halves attack at the same time, red wins.
However, if only one half of the army does, blue wins.

In order to communicate, they use messengers who must pass through the blue territory. This, obviously, results in unreliable communication. However, in order for both armies to agree on a plan, they must gain common knowledge.

1) red 1 sends "attack at dawn"
2) red 2 sends acknowledgement
3) red 1 sends acknowledgement of acknowledgement
4) ...

After which dawn may pass. In an asynchronous system, common knowledge cannot be either gained or lost.

1.3.2Muddy Children¶

G Barnise, 1981

There are $n$ children, playing outside. $1 <= k < n$ children get mud on their foreheads, but they cannot see it themselves. Once they get back inside, their guardian announces that "at least one of you has mud on your forehead. Do you know if you do?"

The children all answer truthfully and collectively "No!" $k - 1$ times. The $k$th time, $k$ children say yes.

The children are building up knowledge incrementally. Each time the question is asked, the children are getting some extra piece of information; that none of the other children say "yes".

If $k=1$, the lone child with mud notices that no one else responds and has mud. So it must be him/her.

If $k=2$, $C_1$ and $C_2$ have mud. $C_1$ sees $C_2$ and vice-versa, but neither say yes in round 1. The other child knows $k \neq 1$, so again, "it must be me."

Assume true for $k-1$. The $k$th time, $C_1$ sees $k-1$ muddy children, but they all say no. The $k$th time, if none of the $k-1$ children said yes, and there are only k-1 other muddy children, "the last must be me." The same applies for the other muddy children.

1.4Distributed Knowledge¶

Helper & Moss, 1990

We can think about knowledge in distributed way.

$k_i \Phi$

Agent $k_i$ knows information $\Phi$.

$D_G \Phi$

The group $G$ has distributed knowledge of $\Phi$

E.g. if $k_1 \alpha$ and $k_2 \alpha$, then $D_G \beta$

$E_G \Phi$

Everyone in $G$ knows $\Phi$

intersection of $k_i$'s knowledges for $k_i \in G$

$S_G \Phi$

Someone in $G$ knows $\Phi$

Union of $k_i$'s knowledges for $k_i \in G$

$E^k_G \Phi$, $k >= 1$

$E_G^1 \Phi = E_G \Phi$

$E_G^{k+1} \Phi = E_G E_G^k \Phi$

$C_G \Phi$

$E_G^1 \Phi \land E_G^2 \Phi \land ...$

For the 2-army problem, we need $C_G \Phi$.
For $k$ Muddy children, we need $E_G^k \Phi$

In message passing, consistency is different; data transfer is explicit.

2Dataflow¶

The idea of Dataflow originates from functional programming. When we think of a functional programming language, each of the boxes are functions, where the state is encapsulated. There are two flavors of dataflow: static dataflow (strict), and dynamic dataflow.

h(f(x, y), g(x, z), y)

If we have a functional computation like the above, we can think of it in a graphical model:

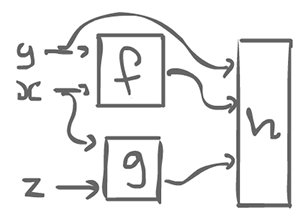
We have some box which computes f, a function which receives 2 inputs, y and x. There is also a box for g which receives two inputs, x and z. y, the result of f and the result of g get get into h.

This suggests a strategy where we think of all the boxes as agents. On the edges (wires) there is some kind of data floating around, tokens that are passed around. An agent waits for available tokens to be input. When it receives enough, it can fire: consume the input(s), compute something, and produce one or more output.

2.1Static dataflow¶

The straight-forward way of doing things, static dataflow puts some constraints. The agents necessarily block (or wait) until all the inputs are available, after which it can fire.

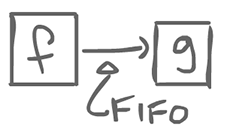
The channels (edges between agents), in static dataflow, are FIFO, lossless, but have bounded capacity (g cannot wait for an infinite amount of tokens).

This actor has 2 inputs and outputs their sum. In static dataflow, agents consume 1 token on each input, and produce 1 on each output. There might be multiple inputs and/or multiple outputs. This is a strong constraint that we could relax a little bit.

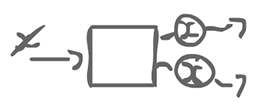
The doubler agent has 1 input, but produces 2 outputs. This is still a regular actor.

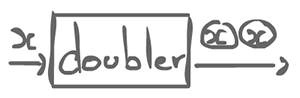
Regular actor

Consumes k_i tokens on input i and produces n_j tokens on output line j for constants k_i, n_j for all i, j.

Homogeneous actor

k_i = 1, n_j = 1 for all i, j.

Even with regular actors, there is some things we cannot do. There are 3 properties that programming languages need to have to be fully expressive:

1. Sequence things
2. Repeat things
3. Produce conditions

1 and 2 are doable, but not 3.

2.1.1How to do a condition¶

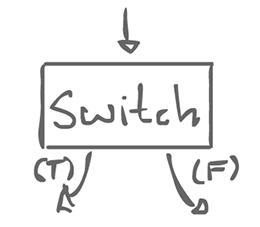
Some input comes in, and there is 1 of 2 possible outputs, a true and a false branch. This is not a regular actor. It always consume a token on input, but on the output, it only sends data on one of either branch.

Maybe all we have to do is give ourselves two special actors that are not regular, but still allow regularity to be enforced as a whole: switch and merge.

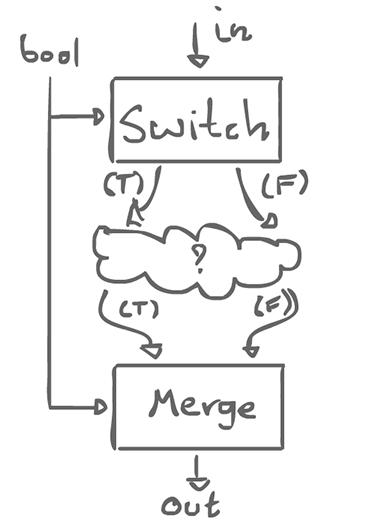
There is also a boolean control input which decides which output line is used.

With these two actors, we can can create a template, an if-schema:

if (bool) {
    f(x);
} else {
    g(x);
}

With this, we can do different things, depending on the boolean control.

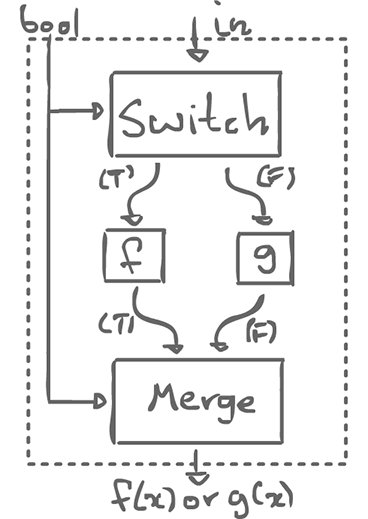
We can draw a box around the whole thing and consider as an agent. It consumes one boolean input, and 1 x, to produce either f(x) or g(x). From the outside, this looks regular, even homogeneous.

2.1.2How to do a loop¶

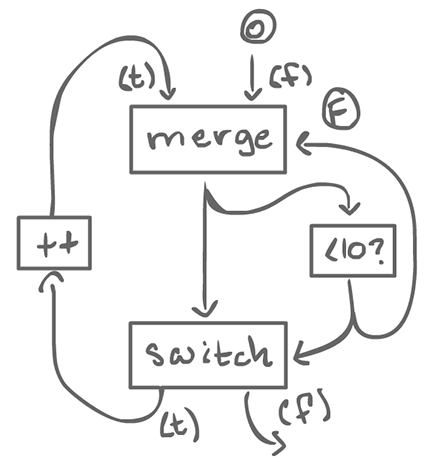
The boolean input of the merge is initialized to false, or else, it does not work.

From the outside, this looks like an homogeneous actor as well. There is an input (the start value of the loop), and an output (the end value of the loop). Also, it is reusable: the boolean input of merge goes back to false at the end of the loop.

To do turn this into something that can iterate a function, we end up with something a bit more complex:

for (int i=0; i < 10; i++){
    x = f(x);
}

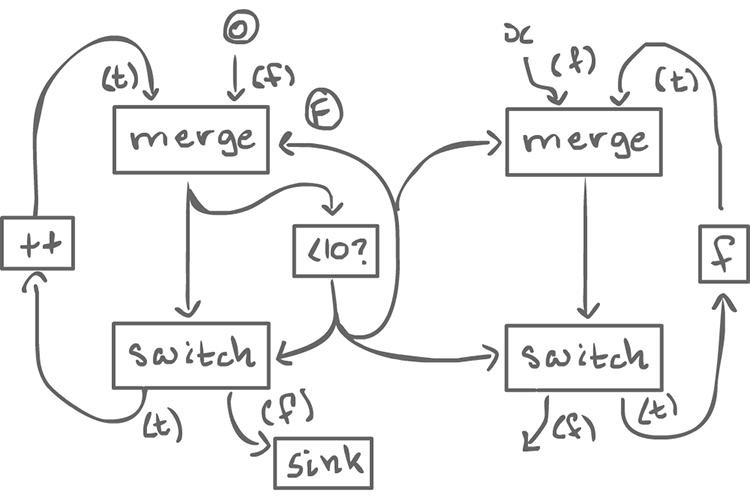
From the outside, it looks homogeneous. In order to destroy the iteration value, we can use sink actor which has 1 input and does nothing.

It is left as an exercise to create a graph which computes f^n(x), given n and x (instead of having n fixed to 10).

2.1.3Calculating channel bounds¶

The nice thing about homogeneity/regularity, is that things are bounded. We do not want an actor with no input at all, but an uncontrollable output which spews out values. If we do have that, we have to make sure there is an actor which consumes it at a reasonable rate.

Assuming regular actors (in the case switch and merge, consider it as a whole)...

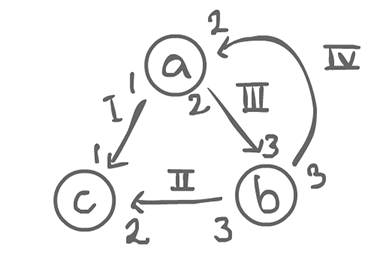
We end up with a system of equations (one equation for each arrow). The number of times a node fires has to match the number of times another node consumes it.

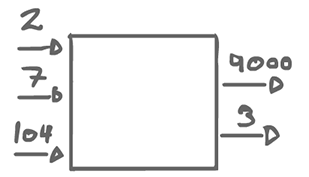
(I)   a = c
(II)  3b = 2c
(III) 2a = 3b
(IV)  3b = 2a

// a = c
3b = 2c
2a = 3b
3b = 2a

// They are all symmetric
2a = 3b

We have to come up with values that make the equations true. Of course, there is the trivial (0, 0, 0), but there is also (3, 2, 3). As a matter of fact, any multiple of (3, 2, 3) works, but the smallest positive value integer is what we are interested in.

So if a fires 3 times, b 2, and c 3, we get a stable state in that the sum of tokens is 0. From that, we can figure out the exact capacity we would need for each edge:

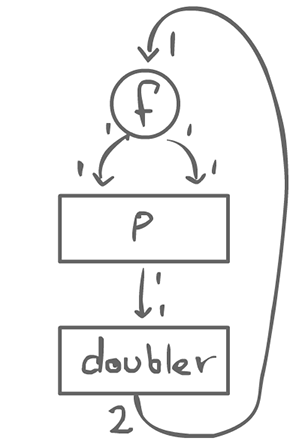
If there is no solution, then the system does not work.

Here is a non-trivial example:
[Insert]