Monday, September 23, 2013

Mutual Exclusion algorithms and linearization

1More Algorithms¶

1.1Ticket Algorithm¶

The ticket algorithm is something really trivial, the inspiration of which comes from real life. When someone walks into a store, or a medical clinic, for example, there usually is a little ticket dispenser. People take a ticket, and wait for their number to be called.

// Init
int next = 0; // The number display
int turn[n]; // Every thread's own ticket
int number = 0; // The next ticket to be taken

// Enter
turn[id] = number++; // This MUST be atomic
while (turn[id] != next); // Spin

// Exit
next++; // Not atomic, but in the thread itself so only this thread does it.

Two threads might read the same number if the line turn[id] = number++; is not executed atomically. We end up having to use mutual exclusion, inside a mutual exclusion algorithm.

1.2Bakery Algorithm¶

Lamport, 1974

The idea of having a centralized ticket dispenser might not be something we want to keep.

What people usually do, when there is no ticket dispenser upon arriving at some place they should wait, is to keep in mind who was there before them, and only take their turn once all these people have taken theirs.

// Init
int turn[n];

int max(int[] arr) {
  // Return the biggest integer in an array
}

// Enter
turn[id] = max(turn) + 1; // This MUST be atomic

for (int i=0; i<n; i++) {
  if (i==id) continue;
  while (turn[i] != 0 && turn[id] >= turn[i]); //Spin
}

// Exit
turn[id] = 0;

Nb 1: We can relax the atomic max operation. A solution, present in the textbook, is the use of "lexicographic ordering": threads, on top of using their respective turn value, also consider their ID. That is, two threads are allowed to end up with the same number, but break their tie by arbitrarily considering their ID as well.

Nb 2: In both the case of the Ticket Algorithm and the Bakery Algorithm, it is possible for the turn/ticket number variable to overflow. It is not much of an issue in the former case because the tickets numbers are compared absolutely, but in the Bakery Algorithm, the numbers are compared relative to the others. There are solutions for that, but it is beyond the scope of this course.

1.3Queue-locks¶

HOLD IT RIGHT THERE. This link explains everything, but better.

1.3.1MCS locks (Mellor Crummey Scott)¶

class Node {
  Node next
  boolean locked
}
// each thread is going to have its own node

enter(Node me) {
  Node pred = TS(tail, me)
  if(pred != null) {
    me.locked = true
    pred.next = me
    while(me.locked) //spin
  }
}

exit(Node me) {
  if (me.next == null) {
    if (compare_and_swap(tail, me, null)) return; // no one else there
    while(me.next == null); // spin (during exit, wow), wait for whoever's coming in to finish
  }
  me.next.locked = false;
  me.next = null;
}

Pros:

• Space-efficient
• Cache-friendly
• First come first served

Cons:

• cas, ts
• Exit spins

1.3.2CLH lock¶

class Node {
  boolean locked
}
static Node tail = new Node()
// each thread will have:
Node me = new Node()
Node pred = null // just a pointer

enter(Node me, Node pred) {
  me.locked = true
  pred = TS(tail, me)
  while(pred.locked) // spin
}

exit() {
  me.locked = false
  me = pred
}

Use pred value to maintain an implicit queue.

Pros:

• fcfs
• Cache-friendly
• Doesn't spin on exit
• mem efficient
• Only uses ts

2Spin-locks in general¶

• easy
• can be less efficient if we're waiting for a while
• blocking (sleep & wakeup)
• synchronized -> blocking
• mutex -> blocking

3How do Java locks work¶

We have seen a lot of locks. We know that in Java, a synchronized block/method locks a mutex, but how is it implemented? If we are doing concurrent programming in Java, we normally end up acquiring locks frequently, in more ways than one. The actual cost of locking becomes a significant concern.

Hybrid lock (combines spin & block)
Actual contention is rare

3.1The lockword in an Object¶

Every Object has a lockword which it uses to keep track of its locking state.

3.2Thin locks¶

Common use-cases (from very common to rare)

• locking an unlocked object (and unlock it)
• shallow (recursive) locking (<= 256 levels): we might try to lock something and call another synchronized method inside the same object, thus acquiring the lock again.
• deep (recursive) locking. Lots of relock of the same object over say, a data structure (e.g. a recursive linked list doing some stuff on the list and locking and locking...).
• shallow contention (one thread waiting for another)
• deep contention (bunch of threads trying to acquire the lock at the same time)

Java optimizes for the first two (more frequent).

n.b. we will need CAS

32-bit lock word:

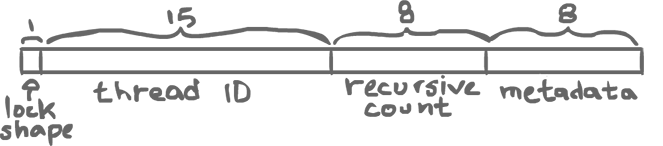
Lock Shape

Either 0 if it is a thin lock (easy cases, above picture), or 1 if it is a fat lock (harder cases, below)

Thread ID

Allows for up to 32767 threads (0 is reserved).

Recursive Count

How many times the lock was relocked through recursion. Allows for a maximum of 256 levels of recursion. After that, a fat lock is required, but a thin lock can accommodate shallow recursive locking.

Metadata

Every object has some header to keep some meta information to keep.

The thin lock form is very cheap to acquire. When the thread ID is 0, it indicates that no thread has acquired the lock. To acquire the lock, in such a case, all that has to be done is a compare-and-swap: CAS(0, [0|id|0|...]);. If the operation succeeds, then the lock is acquired in one atomic instruction.

The operation could still fail. One of the probable cause is that the lock was already acquired by the thread, to do recursive locking. If the ID is already the right one, then all that is left to do is to increment the recursive count, as long as it does not overflow.

3.2.1Locking an unlocked object:¶

(unlocked: all 0s)
cas(lock, 0, id << 16)
if succeed -> locked

Unlock -> get the 3rd field and decrement
  if < 0 -> out
  else start the new count

  if cas fails:
    check the owner. Is it us?
      yes -> recursive locking, then inc 3rd field without overflow then redo

otherwise in all other cases:
  check shape bit:
    if < 1 -> fat lock
    if = 0 -> transition to fat lock
  if we are the owner -> do the transition
  if not -> spin until we are the owner (or it becomes a fat lock), then make the transition

n.b. a fat lock behaves like a normal mutex lock.

3.2.2Fat lock¶

The first two cases described above accommodate the two most common cases, the bulk of locking. In any other case, a thin lock must be transitioned to a fat lock.

The shape bit is changed to 1 and the next 23 bits are used to index an allocated mutex in a table.

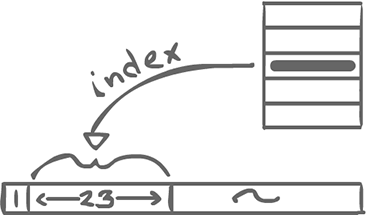
• First section is now 1 (fat lock).
• Second section is now different. Indexes into a table of mutexes. Then we use the mutex from now on. So the transition is one-way. Once you go fat you never go back. (design improved later on (Tasuki locks): allows going back to thin, but uses more data (extra bit))

Nb: There is a little bit of subtlety doing this transition. If a thread already owns a thin lock and needs to change it into a fat lock (i.e. it has exceeded the maximum recursive count), then the transition can proceed. However, if a thread does not own a thin lock and expects to change it into a fat lock, it must spin until the current owner releases it and transition it after.