Wednesday, November 27, 2013

Process algebra and Graphical view

1Process Algebra¶

Very high level abstract algebraic structures trying to represent concurrent programing. The idea behind this is to get to the core of what is happening in concurrent programming.

It deals with interleaving, uses message passing with either synchronous (or asynchronous) messages

Process equivalence

Are two processes doing the same thing or not?

1.1CSP (Communicating Sequential Processes)¶

It has been out for a while, with a variety of different syntactic styles. The idea is to build process expression.

The processes are usually represented by letters. E.g.: $P$ and $Q$.

1.1.1Communication¶

$P:: Q!e$

P sends e to Q

$Q:: P?e$

Q receives a message from P, stores it in e

$e$ can be a variable, or a constant. The types must match.

The communication is synchronous; both $P$ and $Q$ block.

In order for the communication to happen, since $P$ and $Q$ are independent processes and both end up blocking, they must execute in parallel.

1.1.2Execution¶

$P \parallel Q$

Parallel composition operator

Now, P and Q can do their communication

$P::Q!e; x++;$

Sequential composition with the semi-colon.

$P$ sends $e$ to $Q$ and then increments $x$.

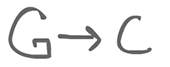
$G \rightarrow C$

Guarded command

$C$ executes if $G$ is true, or if $G$ is a communication, then $C$ executes if $G$ can happen.

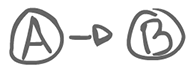
One-shot Producer/consumer example
$$ \begin{equation} A::B!e \\ B::A?e \\ A || B \end{equation} $$

We can also put a single cell buffer in between $A$ and $B$:

$$ \begin{equation} A::C!e \\ B::C?e \\ C::A?e \rightarrow B!e \end{equation} $$

Here, guard and sequential composition are equivalent.

$*[ X ]$

Iteration operator

Iterate $X$ for as long as possible

Until $X$ deadlocks (kind of like a while loop)

1.1.3Choices¶

We would like some way to do some kind of if statements based on the behavior of the concurrency. In order to receive from possibly two different things, there has to be a selection.

$A \Box B$

External choice operator

External choice between $A$ and $B$ (determined by the environment)

Actually a thin vertical box

"do x or y, depending on some external condition"
$A \Box B \parallel somethingParallelWithA$ <- probably will do A

Vending machine exemple
$$ \begin{equation} V:: *\left[ \text{inslot}?1.00 \rightarrow \text{makeTea()} \Box \text{inslot}?2.00 \rightarrow \text{makeCoffee()} \right] \\ V \parallel inslot \end{equation} $$

If 1.00 dollar is inserted, the vending machine makes tea. If it is 2.00 dollars, it makes coffee. After that, it loops back for a new iteration.

$$ \begin{equation} V:: *\left[ \text{inslot}?1.00 \rightarrow \text{makeTea()} \Box \text{inslot}?1.00 \rightarrow \text{makeCoffee()} \right] \\ V \parallel inslot \end{equation} $$

Now, if we put $V \parallel inslot$, the choice is arbitrary and non deterministic; we get either tea or coffee.
So this isn't really an external choice anymore. More like internal. Typically not used since we have an internal symbol (below).

$A \sqcap B$

Internal choice operator

The process internally decides on one branch or the other

Actually a thin box with an opening at the bottom.

$$ \begin{equation} V:: *\left[ \text{inslot}?1.00 \rightarrow \text{makeTea()} \sqcap \text{inslot}?2.00 \rightarrow \text{makeCoffee()} \right] \\ \end{equation} $$

Internally and arbitrarily commits to one side or the other.
If the machine chose to listen to tea only, $V || inslot$ might make tea or it might end up stuck.

1.1.4Distinctions between processes¶

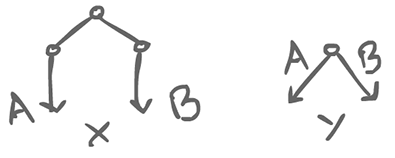
$$ \begin{equation} X::(A?i \rightarrow halt \sqcap B?i \rightarrow halt) \parallel A::(X!42) \end{equation} $$

This may actually use a communication, or it might not. It may end up sitting there, waiting at a communication, or it may reach a halt.

$$ \begin{equation} Y::(A?i \rightarrow halt \Box B?i \rightarrow halt) \parallel A::Y!42 \end{equation} $$

This, on the other hand, will necessarily work.

We can actually look at graph traces:

Back to the buffer: Producer/Consumer

$$ \begin{equation} (P) \rightarrow (B) \rightarrow (C) \\ P::*\left[int x; x = produce(); B!x\right] \\ C::*\left[int x; B?x \rightarrow consume(x)\right] \\ B::*\left[int x; P?x \rightarrow C!x\right] \end{equation} $$

We may have multiple consumers:

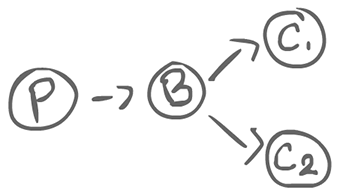
$$ \begin{equation} C_1::*\left[int x; B?x \rightarrow consume(x)\right] \\ C_2::*\left[int x; B?x \rightarrow consume(x)\right] \\ B::*\left[int x, P?x \rightarrow (C_1!x \Box C_2!x)\right] \end{equation} $$

The external event concerns whether $C_1$ or $C_2$ is ready. If both are, then the choice is arbitrary.

$B$ can be seen as a channel between $P$ and $C$. Could it hold more than 1 value? Yes, as a FIFO queue:

$$ \begin{equation} (P) \rightarrow (B_1) \rightarrow (B_2) \rightarrow (B_3) \rightarrow (C) \\ B_1::*\left[int x; P?x \rightarrow B_2!x\right] \\ B_2::*\left[int x; B_1?x \rightarrow B_3!x\right] \\ ... \end{equation} $$

Rather, we might not care about the order:

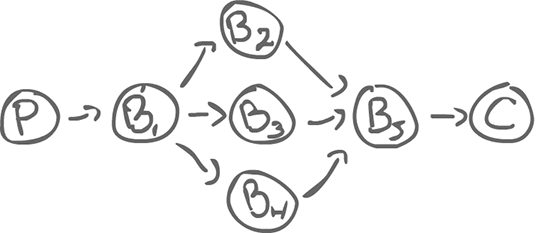
$$ \begin{equation} B_1::*\left[int x; P?x \rightarrow (B_2!x \Box B_3!x \Box B_4!x)\right] \\ B_5::*\left[int x; B_2?x \rightarrow C!x \Box B_3?x \rightarrow C!x \Box B_4?x \rightarrow C!x \right] \end{equation} $$

1.1.5Iterated guarded choice pattern¶

Elevator example
int floor = 1; target = 0;

$$ \begin{equation} E::*\left[b_1?pressed \&\& target==0 \rightarrow target = 1 \Box \\ b_2?pressed \&\& target==0 \rightarrow target = 2 \Box \\ \vdots \\ target!=0 \&\& target>floor \rightarrow floor = floor + 1 \Box \\ target!=0 \&\& target<floor \rightarrow floor = floor - 1 \Box \\ target==floor \rightarrow door!open \rightarrow door?closed \rightarrow target=0\right] \\ door::\left[E?open \rightarrow \dots \right] \end{equation} $$

Iteration has an ugly syntax. Rather, we should use recursion instead. e.g. $P::int x; x=produce(); B!x \rightarrow P$ and $C::int x; B?x \rightarrow consume(x); C$

1.2Java CSP and the graphical view¶

Processes become objects. They run in separate threads. They listen for messages coming in; processes communicate via channels. The processes are then parametrized by the channels. Rather than saying that we have a process $P$, we have process $P(B)$.

For example: P(B)::... where B is the channel name.

The channels can be FIFO, bounded, etc...

In the end, this lets us build up a graphical view of concurrency.

$Identity(in, out)::in?x \rightarrow out!x \rightarrow Identity(in, out)$

$inc(in, out)::in?x \rightarrow out!(x+1) \rightarrow inc(in, out)$

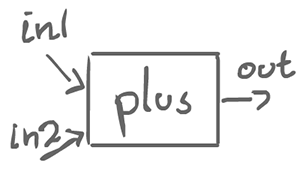
$plus(in1, in2, out):: in1?x \rightarrow in2?y \rightarrow out!(x+y) \rightarrow plus(in1, in2, out)$

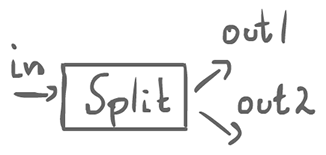
$split(in, out1, out2)::in?x \rightarrow out2!x \rightarrow out1!x \rightarrow split(in, out1, out2)$

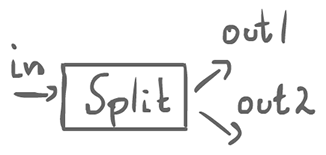
Send in parallel instead
$split(in, out1, out2)::in?x \rightarrow (out1!x || out2!x) \rightarrow split(in, out1, out2)$

Nb: Java CSP has external choice only! Still, choices can be prioritized, be truly randomized, have a fairness property imposed, or have timer guards.