Wednesday, October 16, 2013

Semantics of condition variables, Java's implementation of locking and the Readers and Writers Problem

1Expressiveness¶

Let's look at the expressiveness of some of the primary operations we have been looking at, in a way to try and understand how some of our concurrency primitives for locking behaviors might actually be better or worse than other ones.

We have already seen a lot of concurrency primitives such as atomic variables/registers as well as special instructions like test-and-set, test-and-test-and-set, fetch-and-add and compare-and-swap.

Based on these, we have some locking approaches. The special instructions do slightly different things, some of which are better in certain circumstances. It's easy to build a test-and-set lock, even easier with a compare-and-swap as the if is embedded inside of it; fetch-and-add is good for atomic increments, decrements.

Given only these concurrency primitives, we can build anything. For example, the filter lock only used atomic variable. With it, a test-and-set operation can be built by locking the test-and-set section as a critical section.

Compare-and-swap can be built with test-and-set. The process is to create a basic spin lock and use that to lock some global piece of data, making sure that what is done in the critical section is mutually exclusive to anyone else.

int CAS(int &x, int a, int b) {
    bool rC;
    while (TS(cas_lock, 1) == 1); // Spin
    if (x == a) {
        rC = true;
        x = b;
    } else {
        rC = false;
    }
    cas_lock = 0;
    return rC;
}

In one perspective, there is no difference between the special instructions. Once a lock is built, anything can be done. Expressiveness is not much of a concern in this respect. However, there is one kind of unsatisfying property, that of the spin lock.

The spin lock makes it that a thread may spin for an arbitrary long amount of time, yet that is not a property that compare-and-swap had originally. Compare-and-swap is supposed to be an atomic operation which finishes in a finite amount of time, irrespective of any other thread. That is, even if another thread crashed, it would still finish. It is fault-tolerant.

That is not true of our makeshift solution. If another thread fails for whatever reason, then a thread can be stuck forever. Can we build Compare-and-swap in a wait-free way?

Wait-free operation

Finite number of steps

Fault-tolerant

Simply using a lock cannot create a wait-free operation.

1.1Consensus¶

We have n processes/threads, each starting with a different value, and we want them to all agree on a value, that is, to achieve consensus.

Requirements

Consistent: At the end of the protocol, all should agree.

Valid: The agreed value is one of the input values. It cannot be an arbitrary value.

Wait-free

The consensus problem can be solved for a certain number of processes or threads, but not necessarily for an arbitrary one. As such, concurrency operations can be distinguished by their consensus number.

Consensus number

Maximum number of processes for which a concurrency primitive can solve consensus.

For simple atomic read and write operations on atomic variables/registers, the consensus number is 1.

1.1.1Proof¶

We can think of a protocol with a binary consensus. That is, the number is 0 or 1, with 2 threads. In any protocol that we have, we start out with some state where the agreed value could either be 0 or 1. From this state, maybe Thread₀ or Thread₁ might make an action.

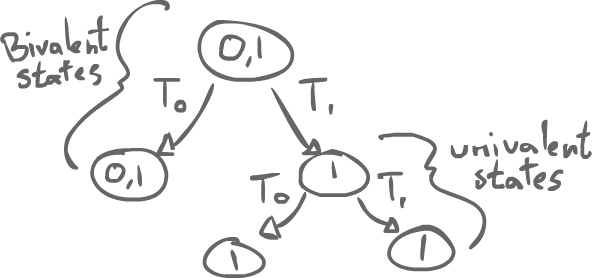
We can start thinking about the state-space evolution of the program. After Thread₀ does something, there is still no agreement: it could be 0 or 1. Maybe, after Thread₁ does something, Thread₀ might do something to finish the protocol, but at a certain point, if this is solving consensus, there should be a state where a value is committed. At any state after that, the same value will still be committed.

Bivalent state

A state where there are two possible values

Univalent state

A state where there is only one possible value

The idea of a wait-free algorithm is that after some sequence of actions by Thread₀ and Thread₁, we should reach a point, starting form a bivalent state, where we end up in an univalent state.

1.1.1.1Critical State¶

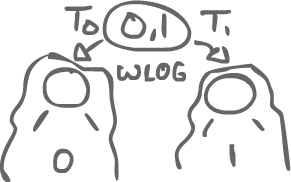
A critical state is the lowest bivalent state in a protocol (last to happen). That is, all subsequent states are univalent. We reach some point where the state is bivalent, but no matter the choice that is made, we end up in a tree of univalent states.

Back to the proof, suppose we have a bivalent critical state.

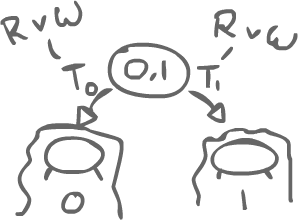
If we only have atomic variables/registers, the only thing that could be done in that critical state is read or write some data. To change to a different state, then either Thread₀ did a Read-or-write first, or Thread₁ did one first.

Case A) Thread₀ reads first, and Thread₁ does something (read or write)

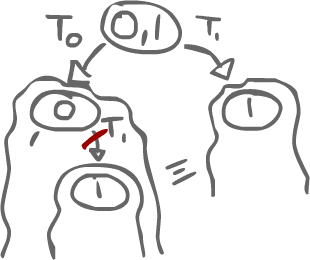
If Thread₀ is doing a read, then that does not matter to Thread₁ as no data is changed. That action is not visible to Thread₁. As such, if Thread₀ reads first, then we should end up in the 0-subtree. However, since the read is invisible to Thread₁, then its action should end up in the same subtree as that of doing its action at the critical state. This is a contradiction, so Thread₀'s action cannot be a read.

Case B) Thread₀ writes x, and Thread₁ writes x as well.

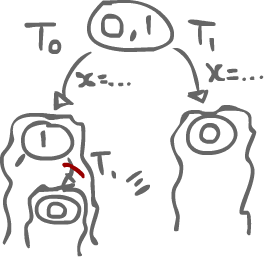
If they write to the same variable, then we have the same problem as in case A. Since Thread₁'s action does not need x's value, Thread₀'s action is again invisible. Thread₁ could simply overwrite what Thread₀ did. Just like in Case A, we end up with a contradiction.

Case C) Thread₀ writes x, and Thread₁ writes y.
This is left as an exercise.

With all things considered, an atomic read-or-write cannot solve consensus for 2 or more threads. As such, it can only reach consensus with a single thread.

1.1.2With Test-and-set¶

We can solve consensus with 2 threads using test-and-set.

// Return agreed value, input value unique to a thread
int decide(int input) {
    int x = TS(decider, input); // Decider is initialized to SPECIAL_VALUE
    if (x == SPECIAL_VALUE)
        return input;
    return x;
}

With test-and-set, we can make up one SPECIAL_VALUE that we initialize the variable decider to. We can then do test-and-set and see if it's that special value. If a thread does not get that special value, then another did it before. If it does get it, then it was the first to do test-and-set.

Test-and-set, Fetch-and-add and a lot of others have a consensus number of 2. Compare-and-swap, however, has a consensus number of theoretically $\infty$ (practically, a very big number). It is significantly better than anything else out there.

int decide(int input) {
    CAS(decider, SPECIAL_VALUE, input); // Decider is initialized to SPECIAL_VALUE
    return decider;
}

What goes on is that if the decider variable is equal to SPECIAL_VALUE, then the first thread can set it equal to its input. After that, any other thread will fail CAS's condition, and so will return decider, just like the first thread. That is, all the threads will return the same value.

2Splitter¶

Something something renaming algorithm (check Art of Multiprocessor Programming, p.44)

Imagine a grid of squares like this one. Actually, more like a grid:

x = id
if (y != 0) RIGHT
else y = id
    if(x != id) DOWN
    STOP