Wednesday, October 2, 2013

Semaphores and Monitors

1The Dining Philosophers Problem¶

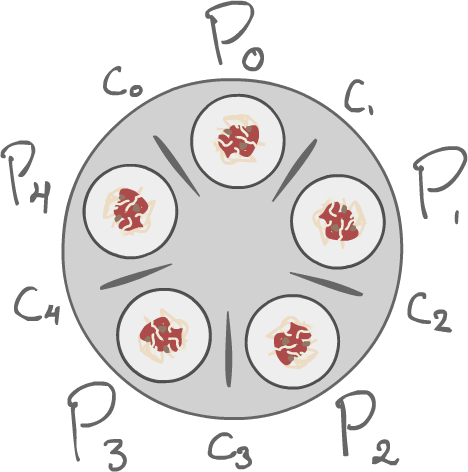
The dining philosophers problem is a classic problem. There are 5 philosophers sitting at a table. They each have a plate and 5 chopsticks are laid out between those plates. The philosophers can either think, or eat using the two chopsticks right next to each of them. These philosophers can actually be modeled as threads:

public class Philosopher extends Thread {
    private void think() {
        // Think for a while
    }

    private void eat() {
        // Eat with their two chopsticks
    }

    @override    
    public void run() {
        while (true) {
            think();
            -> Get hungry
            -> Acquire two chopsticks
            eat();
            -> Release the chopsticks
    }
}

We have 5 philosophers doing this. We have to somehow make sure that when one acquires two chopsticks, another cannot take any of those two chopsticks before the first one releases them.

How can we do this? We will look at some solutions, incrementing from the ground up.

1.1Method 1: Single global lock¶

// In the while loop of each Philosopher P_i (0 <= i <= 4)
think();
lock(globalLock);
-> Take two chopsticks
eat();
-> Release the chopsticks
unlock(globalLock);

Thus, acquiring the chopsticks, eating and releasing the chopsticks becomes a critical section. While this works and is correct, it is not concurrent! There is no reason for, say, Philosopher₀ to block Philosopher₂ from eating because they don't even share any chopsticks. This solution is not concurrent.

1.2Method 2: "Classic solution"¶

Instead of a single global lock, let's associate a lock with every single chopstick.

// In the while loop of each Philosopher P_i (0 <= i <= 4)
think();
lock(chopstick[i]); // Right one
lock(chopstick[(i+1) % 5]); // Left one
eat();
unlock(chopstick[(i+1) % 5]);
unlock(chopstick[i]);

Sadly, this does not work. Say each philosopher acquires their right chopstick one after the other. After that, the first one will not be able to acquire its left chopstick and the same goes for all the other philosophers. The philosophers are stuck; we find ourselves with a deadlock.

The problem is that the operation of acquiring both the locks is separated in two. Instead, it should be indivisible.

1.3Method 3: Global lock mixed with the individual locks¶

// In the while loop of each Philosopher P_i (0 <= i <= 4)
think();
lock(globalLock);
lock(chopstick[i]); // Right one
lock(chopstick[(i+1) % 5]); // Left one
unlock(globalLock);
eat();
lock(globalLock); // This is actually useless
unlock(chopstick[(i+1) % 5]);
unlock(chopstick[i]);
unlock(globalLock); // This is actually useless

This still results in a deadlock, however. Say Philosopher₀ starts by locking the global lock, acquires both its chopsticks and unlocks the global lock. Then, Philosopher₁ locks the global lock and tries to acquire its first chopstick, but ends up being stuck. Then, Philosopher₀, who is done eating, tries to lock the global lock, but Philosopher₁ still has it! We, again, find ourselves with a deadlock.

Locking the global lock when unlocking the chopsticks' locks is actually useless; it does not make much sense to lock the unlocking process.

1.4Method 4: Strike out the lock/unlock global when releasing the chopsticks¶

Not locking the global lock during the unlocking process avoids the deadlock, but it is still suboptimal, because it limits concurrency. In effect, there is a scenario where a philosopher who could eat still ends up waiting. Finding it is left as an exercise.

(Screwed up here, will fix)

1.5Method 4: Global lock when locking only¶

think();
lock(global);
lock(chopstick[i]);
lock(chopstick[(i+1) % 5])
unlock(global);
eat();
unlock(chopstick[(i+1) % 5]);
unlock(chopstick[i]);

This does not deadlock, but it is suboptimal in the sense that we don't get great concurrency. Here's a trace that shows this lack of efficiency:

// Philosopher 0
lock(global);
lock(chopstick[0]);
lock(chopstick[1]);
unlock(global);
eat();

// Philosopher 1
lock(global);
lock(chopstick[1]); // Stuck

Philosopher₁ is not stuck forever, only until Philosopher₀ finishes eating, but he cannot grab chopstick[1] because Philosopher₀ has it. All the while, Philosopher₁ still has the global lock! As such, even though Philosopher_{2, 3 (or even 4)} could readily eat, they cannot even start grabbing chopsticks because Philosopher₁ blocks them.

1.6Method 5: Randomization¶

What produces the deadlock situation is that all the philosophers are systematically grabbing the left chopstick, then the right. What if, instead of always using the same ordering, we would randomize it? Sometimes, a philosopher could grab the right chopstick, then the left. Other times, he could grab the left chopstick, then the right.

We end up breaking the symmetry, which allows to not necessarily end up with the same situation as before. However, we could still be unlucky: it is statistically possible that we end up with the same situation as before. As such, this solution is more likely to work better, but it is certainly not guaranteed to do so. That is not something we really wish for, in concurrent programming.

1.7Method 6: Only let 4 philosophers sit at the table at any one time.¶

Another problem is that there are not enough chopsticks to go around. With all 5 philosophers sitting down, there simply are not enough chopsticks to let all the philosophers eat at the same time. If we let only 4 philosophers sit down at one, then maybe we could actually solve this problem.

Indeed, if only 4 philosophers sit down, there should be at least two chopsticks for at least one philosopher.

// Philosopher i
-> try to sit (atomically decrement)
lock(chopstick[i]);
lock(chopstick[(i+1) % 5]);
eat();
unlock(chopstick[i]);
unlock(chopstick[(i+1) % 5]);
-> give up the seat (atomically increment)

The operation to try to sit involves keeping track of how many free seats there are. There are 4 seats at first; atomically, a philosopher could take a seat, but not take one if the number is 0. This is not something that can be done in a single statement necessarily, and it would need an extra bit of work to implement:

boolean temp;
do {
    lock(global);
    temp = false;
    if (seat > 0) {
        seat--;
        temp = true;
    } unlock(global);
} while (!temp);

Basically, the fifth philosopher who comes along and tries to sit down after everybody else will be stuck there spinning. Semaphores would make this even more trivial, but it is already possible to do it with spin locks.

At the end, the philosopher needs to atomically re-increment the number of seats. This can be done with a global lock, or with a fetch-and-add primitive.

The solution does work. We cannot get in a deadlock situation because the last philosopher cannot block anymore because of the first; the fifth, un-sit philosopher will always leave a hole for a chopstick to be available.

1.8Method 7: Acquire and release¶

Instead of grabbing a chopstick and holding on to it until he gets the next one, a philosopher could grab one and then try to grab the other. If unsuccessful, he would release the first, then start over.

1.9Method 8: Order the resources (best solution)¶

The chopsticks are already ordered. However, they are not always acquired in order; Philosopher₄ tries to acquire the last chopstick, then the first. This philosopher should rather pick the chopsticks in the opposite order.

It is a bit like the randomization solution, except it is not actually random. One philosopher in particular is going to break the symmetry, and it is impossible to get back to the deadlock situation.

2Resource Deadlock¶

2.1Coffman's conditions (1971)¶

There are resources in a programs/computer that threads or processes try to acquire. As they compete for acquiring the resources, we may end up with deadlocks. There are 4 conditions necessary to generate a resource deadlock. If we make sure that a program does not meet one of those conditions, then we are assured not to get deadlock.

2.1.1Serially usable resources¶

The processes/threads share resources, which they need under mutual exclusion. That is, if one philosopher has a chopstick, no else is supposed to be able to have the same chopstick.

2.1.2Incremental acquisitions¶

The serially usable resources are picked up one at a time. That is, two chopsticks are needed, but they cannot be grabbed both at at once.

2.1.3No preemption¶

Once a resource is held, only the process/thread holding it can let it go. That is, a philosopher cannot ask another next to him to hand him his chopstick.

2.1.4A dependency cycle exists¶

There is a circular chain of processes/threads, each holding a resource the next needs in the chain.

2.2Getting rid of a condition¶

Often, condition 1 and 2 are actually built in the problem we are facing. We may not be able to change these 2 conditions without changing the problem itself. Condition 3 and 4, however, are better ways to approach the problem.

As for condition 3, there is a solution (not listed) to the Dining Philosophers problem where the philosophers are allowed to steal chopsticks from each other.

Typically, the easiest way is to get rid of of dependency cycles (i.e. solution 8). This is the solution that should come to mind first.

To do this, resources have to be ordered:

We can also think of it as a chain of dependency:

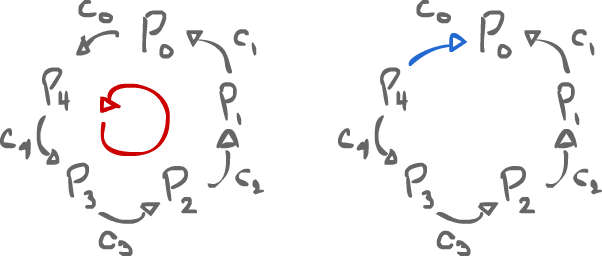
There is a cycle in the first diagram, but it is broken in the second, once the resources are ordered. We don't end up with a cycle anymore.

We must always make sure that, when we need to acquire multiple resources, we acquire them in order. This way, we never end up with dependency cycles (but rather a tree). Sometimes, the resources are too hard to order, but in most cases, this will work really nicely.

Nb: the ordering is arbitrary, but everyone needs to agree on it. It can be a total order, where everything is comparable to everything, but it can also be a partial order (as long as we can distinguish between two resources which one is bigger that the other one).

2.3Other kinds of deadlocks¶

We've seen what resource deadlocks are. They are deadlocks based on acquiring resources, but there are other kinds of deadlock. For example, imagine two train tracks crossing, with the two trains riding them being on a collision course.

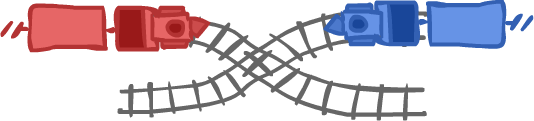
They cannot be in the intersection at the same time. If the drivers are cautious, then they will both stop, seeing another train is coming. Neither acquires the "resource". Yet, they end up stuck, waiting for each other. The same may happen with human beings when getting in and out of a room at the same time, or when walking on the same side of the sidewalk.

2.3.1Livelock¶

A livelock is not the same as a deadlock. When a deadlock occurs, no one can make any progress; everybody is stuck. During a livelock, at least some thread is doing something, but it is useless; no one is making actual progress on the problem to solve. That is, in spite of doing something, the program is still stuck.