1Linearization¶
What is a correct concurrent program? Concurrent programs are not necessarily functional! Sequential execution can only happen in one way. As for a concurrent program, the outcome depends on the order of execution.
In a sequential program, if m1() executes before m2(), there is no way for m2() to start before m1() finishes. There is a nice kind of ordering which is very clear and well defined
In a concurrent program, if there are two threads, one executing m1(), and the other, m2(), these function will happen over two certain spans of time which may overlap in some way. This makes it harder to think about.
Idea: If all function have a single point in time when they take effect (e.g. set a certain variable), then it is easier to map to a sequential execution by handling those function by this point, the linearization point. Now, we just have to think about the interleaving of the linearization points.
1.1Formalization of the idea¶
Herlihy and Wing, 1990
They tried to formalize the idea, with respect of correctness, thinking in particular of abstract data types (ADTs).
If we have a concurrent program, in order to reason about it, we find these linearization points (actually the easiest part of linearization), but we also want to make sure that the operations, what the functions are doing make sense in a certain order.
If the ordering of the linearization points match the required ordering for the operations on the ADTs to make sense, then the program can be claimed to be correct.
1.1.1Definitions¶
There are operations that are going to happen. These operations depend on the thread that execute them, the variables they are operating on, objects and ADTs, and on the methods they are calling, or even whatever read value they get back.
As such, there are some sort of tuple that we can think of as events that will happen inside the program. These tuples will form some sort of history.
The idea is to look at various histories and see if it is a valid history for a program. If one can be constructed such that it matches the way the program is supposed to work, then the program can be said to be correct.
- History
- A history $H$ is a sequence of method invocations and responses.
Different invokes will match up if they are executed by the same thread on the same object.
In a certain history, we might have pending invokes (no response yet), when we are looking at fragments of execution.
If that is the case, we should be able to extend the history to append all matching responses to pending invokes.
- Complete History
- A history $H$ is complete if all the invokes are matching a response.
- Sequential History
- A history $H$ is sequential if the first event is an invoke and each subsequent invoke is followed by its response (except maybe the last invoke.)
- Sub-histories
- A history $H$ can be filtered by some thread, or object. That is, a sub-history is the result of taking only the events corresponding to some thread $T$ or some object $x$: $\left.H\right|_T \text{ or } \left.H\right|_x$
- Well Formed History
- A history $H$ is well formed if for all thread $T$, $\left.H\right|_T$ is sequential.
- Nb: Nested method invocations are hard to model here.
- Linearizable History
- A history $H$ is considered linearizable if it has an extension $H'$ and there exists a sequential history $S$ such that:
$$ \begin{equation} \begin{split} \text{a)} &\text{ } H' \equiv S \\ \text{b)} &\text{ } \text{if } n_i \rightarrow n_j \text{ in } H \Rightarrow n_i \rightarrow n_j \text{ in } S \end{split} \end{equation} $$
This says that we have some trace of events, and that trace of events can be seen to be the same as a sequential execution: any operation, any dependency due to the ADTs, and all the orderings are still preserved.
2Linearization review¶
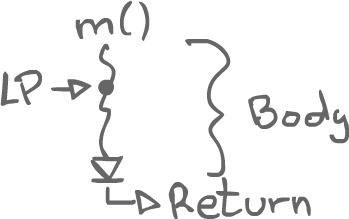
In sequential programs, if two methods calls are done in a row, then one happens before the other. With concurrent programs, however, we have to start thinking about the span during which the methods execute as they now generally overlap. The key idea of linearization is to think of the methods as having linearization points. If we can say there's a particular point, such as an assignment to a variable, that makes a method call finally take effect, then the method call can be seen as a point rather than a span.
Correctness of abstract data types operations is also a key concept. Not only do we have to care about the linearization points, we also have to make sure that the concurrent executions correspond to something that makes sense with respect to ADTs. For example, taking something out of a queue should not happen until something has been inserted first. That is, the linearization point of a method taking something out of a queue should happen after the linearization point of a method that puts something in the queue.
We start thinking about the history of a program as a series of events where a method is called, and then the method returns. There is a kind of behavior which matches invokes and responses, and the idea is that there is a linearization point somewhere in between these events take place.
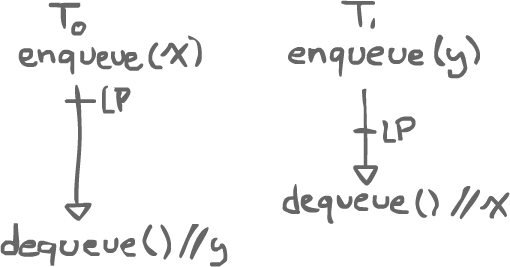
Say Thread0 and Thread1 have access to the same FIFO queue. Thread0 enqueues a value x, which takes a certain time. At the same time, Thread1 enqueues another value, y. Then, Thread1 dequeues something and happens to get x. Finally, Thread0 dequeues something and gets y.
Since we are dealing with a FIFO queue, there is an ordering that makes sense: the first thing dequeued should be the first thing enqueued. There is also an ordering that does not make sense. In order for x to be the first dequeued item, the linearization point of Thread0's enqueue should be above that of Thread1's. We have to think of the ordering of the linearization points in a way that makes sense with the ADTs.
There is, in this case, a sequential interleaving that does make sense:
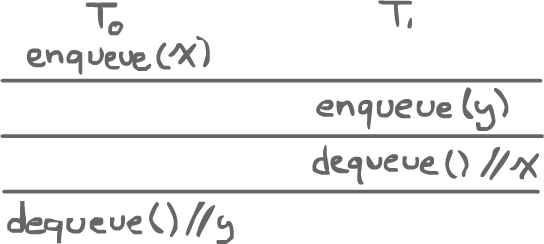
If it is impossible to come up with a sequential history for a program, then the program is not linearizable.
3Scheduling¶
In concurrent execution, we are letting threads run, but we do not know how fast they run! That is up to the operating system, and the underlying hardware, on top of which time slicing issues can appear. So there is no way to guarantee the speed of each thread. In a kind of abstract way to represent this, we can think of threads executing at arbitrary speed. Threads might run very slowly, or very rapidly, yet programs should be correct in spite of those variations.
3.1Safety vs. Liveness¶
Safety is something that can be guaranteed. Once we analyze our locking code and our mutual exclusion algorithms, we can convince ourselves that things are guaranteed to be safe. Convincing ourselves that things are actually live, that threads will execute, make progress that happen, is something where we have to start thinking about whether our threads are executing, at what speed, and whether they actually get a chance to do so.
Scheduling is one of the reasons why liveness ends up being a tricky problem; liveness often depends on scheduling. We already know that in Java and PThreads, we may get a nomally priority preemptive policy, but we don't get a lot of guarantees.
boolean go = false; // This should actually be 'volatile'! // Thread 0 while(!go); important(); // Thread 1 go = true; stuff();
What is supposed to happen inside here, is that we are setting a kind of one-way little barrier. We want to make sure that Thread0 does not progress into important() until Thread1 actually sets go = true;.
However, there's already one flaw in this. The boolean go should be declared "volatile". If the compiler looks at the program, trying to improve it, it will look at go being false, and see the while which tests if go is false. Since the value of go, in a sequential mindset, does not change up until the loop, then there is supposedly no need to check for the value of go at all; the loop could effectively be interpreted as an infinite loop and be replaced by while (true);.
There's another reason why it might not actually work. Maybe this program will run on a single CPU system that does run-to-completion, a policy which does not use time slicing. Java does not necessarily guarantee time slicing! What is possible to happen is that Thread0 will execute its loop infinitely and Thread1 will never even get a chance to execute.
3.2Fairness¶
We need an abstract guarantee that all the threads will be able to execute. It becomes an issue of fairness. In the last program, Thread1 should have a chance to execute eventually. If there is a guarantee that Thread1 has a chance to execute, then the program can be shown to actually work.
There are a few levels of fairness that are certainly interesting to study:
3.2.1Level 1: Unconditional fairness¶
This is probably the lowest, most minimal level of fairness we can imagine in a concurrent system.
A scheduling policy is unconditionally fair (UF) if every unconditional atomic action that is eligible to execute eventually is executed.
'Unconditional' means that it is not waiting on anything. An unconditional atomic action is a statement that we can execute. 'Eligible' means that some thread program counter is sitting at such a statement, ready to execute.
That is exactly what we had with Thread1. Its statement go = true; is something we can look at and consider that there is no condition, that it is not waiting after anything else to execute, that it is an atomic action, and that it is eligible. In an unconditionally fair system, it would be possible to assert that, no matter the scheduling issues, Thread1 will actually get to execute go = true;.
3.2.1.1Conditional atomic actions¶
On such a system, however, although Thread0's while (!go); contains an unconditional atomic action (the check for go), the whole statement is not guaranteed to be executed fully in order to let the thread into the important(); part.
To counter this problem, people came up with the construct of conditional atomic actions. The idea of it is that a thread wants to wait for something to be true, and then do something. That is kind of what is done in the program (waiting for go to be true, then do important();). In general, we want to be able to check for the condition and execute something else after atomically.
wait(B); C(); // Wait for B to be true, then execute C // During which B is unchanged by anyone else.
While C is executed, B does not change; it is all atomic. The program can now be rewritten differently to use a conditional atomic action.
volatile boolean go = false; // Thread 0 wait(go); important(); // Thread 1 go = true; stuff();
3.2.2Level 2: Weak fairness¶
The unconditionally fair policy does not guarantees to execute conditional statements fully. Slightly stronger than unconditional fairness, there is weak fairness. It basically does the same, only it also allows for conditional actions.
A scheduling policy is weakly fair if a) it is unconditionally fair and b) every conditional atomic action that is eligible is eventually executed assuming its condition becomes true and remains true until seen by the process executing the conditional action.
In a weakly fair system, the program above is guaranteed to work. However, the go variable only changes once. Instead, one actually can imagine a situation where the flag might toggle:
// Thread 1 while (true) { go = true; stuff(); go = false; moreStuff(); }
Thread1 is basically sitting in a loop and toggling go. Now, we don't have a guarantee that Thread0 will be able to see go changing to true and execute its important(); part. Realistically, we don't expect variables to change only once as in our past trivial program. It is expected for variables to change often, so we need a stronger level of fairness
3.2.3Level 3: Strong fairness¶
Strong fairness will assert that even if Thread1 is doing something like toggling go, Thread0 will eventually get to execute when go's value is true. This is something to be frankly, quite hard to guarantee in practice.
A scheduling policy is strongly fair if a) it is unconditionally fair and b) every conditional atomic action that is eligible is eventually executed assuming its condition is true infinitely often.
However, a strongly fair scheduling policy, which guarantees Thread0 to execute, is not feasible in practice. A scheduler knows nothing about the programs executing; how could it know how to schedule the threads properly?
Since no such scheduling policy exists, there is no guarantee that every concurrent program will actually work.
4Race conditions¶
A race condition is considered an error in concurrent programming. Race conditions are not always bad, however, as all the low-level locking algorithms we have seen are actually built on race conditions. So, at some very low level, race conditions are necessary, but at any higher level, programs should not have race conditions.
Often, a race condition is, to some degree, mistakenly interpreted as a problem which has something to do with non-determinism. For example, let's have the variable int x; and Thread0 execute x = 1; while Thread1 executes x = 2;. The speed of execution determines the outcome; the value of x is either 1 or 2 depending on which thread executed their respective statement first. There is, in effect, a race condition, as the threads are racing (to be last) and have their value persist.
This interpretation is not quite true, however. The program does have a race condition, but such an outcome itself is not always caused by race condition! For example, if we keep that last program the same, but put the threads' assignments in synchronized blocks:
int x; // Thread 0 synchronized (lock) { x = 1; } // Thread 1 synchronized (lock) { x = 2; }
Then, the outcome, the value of x, will still be 1 or 2 depending on which thread executed their statement first, but this time, there is no race condition. The behavior is kind of the same, but since the statements are placed in synchronized blocks, the actions are still well ordered, even though this order depends on timing at run time.
So, a race condition is not a problem with non-determinism, it is rather a problem caused by actions that are not well ordered. Non-determinism is not necessarily a problem in concurrent programming, although it does make programs harder to understand.
4.1Orderings¶
4.1.1Intra-thread order¶
Firstly, there is the normal control flow within a thread. That is, there is a control flow that defines the order in which the actions are done that respects the program order.
// No surprise in the order of the actions here a = b; c = d; if (x) { A(); } else { B(); }
This is what is called intra-thread ordering. Within any thread, we have normal control flow. Within a single thread that executes a program, the statements are executed sequentially.
4.1.2Synchronization order¶
There is another kind of ordering within concurrent programs because we are dealing with interactions between threads. The synchronization order is the ordering of synchronization actions; it does depend on the semantics of what the sync action actually mean.
If Thread0 locks x and then unlocks it, another thread cannot acquire the lock at the same time. Therefore, at run time, only one synchronization order can happen. Either Thread0 locks and unlocks x before Thread1 or vice-versa.
In Java, there is also a synchronization order between volatile variables. For example, if we declare volatile int x;, after which Thread0 executes x = 1; and Thread1 executes x = 2;, then there is a synchronization order between those two statements; one of them will happen first at run time.
Without that volatile keyword, the synchronization order is not there. The two statements would not be ordered anymore. There is no synchronization order with data races!
- Data race (better definition)
- A data race in a multi-threaded program occurs when two (or more) threads access the same memory location, without any ordering constraint, and at least one of them is a write.
4.1.2.1Why do we care about this synchronization order¶
The reason why synchronization ordering is important is because we want to make things visible to the hardware and to the concurrent system. The hardware knows that when we lock things, using special locking instructions in the hardware or with the software (using synchronized), we are doing something that another thread needs to know about. As such, the hardware has to make sure that what has just been done needs to be visible to other threads. Otherwise, nothing special would be done with the registers and the cache. As such, our synchronization methodology interacts with how the program is compiled to more efficiently use the hardware.
5Deadlocks¶
Deadlocks occur when threads are stuck waiting after each other. Then, the whole program freezes up as everybody is waiting after everybody else and the program does not make any progress.
6Java Concurrency utilities¶
Java has a fairly rich library of high level concurrency constructs, available in the java.util.concurrent.* package. All those features could be implemented on our own using basic constructs. Here are some of the main features:
6.1Callable<V> interface¶
Instead of just having Runnable, we also have a Callable<V> interface. The problem with Runnable is that the run() neither takes any arguments nor returns any value. That is, in order to share data, it had to be stored somewhere else. Callable<V> actually returns something and can also throw exceptions.
6.2Executor¶
An Executor gives us an high-level access to doing tasks in parallel (with or without threads). Tasks (Runnable or Callable) are fed into an Executor and it does them. There is an Executor class that acts as a factory by instantiating executor services. There are many different implementations:
- Thread pool Executor
- Defining a min/max of threads, we can feed tasks to this executor and it will use threads to execute them as concurrently as it possible can (with an at least
min, at mostmaxnumber of threads). - Cached Thread pool Executor
- Maintains some number of threads (it adaptively decides how many threads it should use).
- Fixed Thread pool Executor
- Where the number of threads is fixed. Given a number of threads, it will never use less or more than this number.
- Single Thread Executor
- Executes everything with exacly one thread, executing all the tasks sequentially.
- Scheduled Executor
- Executes tasks in a scheduled fashion, to be repeated at some frequency.
6.2.1Futures¶
When we pass a task to an Executor, how do we know once it is actually done? What an Executor returns is a Future object, a promise to do something in the future: f = new Future(task);. It has a f.get() method which either returns what the task ended up returning, or makes the caller wait if it has not yet been executed.
6.3Semaphores¶
Java does not originally have semaphores. We can build them, but java.util.concurrent.* provides some classes for that.
6.4Barriers¶
- Countdown Latch
- A one-shot barrier
- Cyclic barrier
- A reusable barrier (there is a
reset()method) - It has the ability to use a barrier thread which gets executed once all the other thread has gotten to the barrier point, before everyone is released.
6.5Concurrent Data structures¶
ConcurrentHashMapConcurrentLinkingQueueBlockingQueue: Fixed size, wait if full- ...
6.6Locks¶
In java.util.concurrent.locks there are explicit locks; we do not have to always use synchronized blocks. A Lock is used very much like a mutex in PThreads. There are also condition variables with every every lock: Lock.newCondition() -> Condition. There are also ReadWriteLocks which give us a solution to the Readers Writers Problem by having a read lock which can be locked multiple time, and a write lock which can only be locked once at a time.
6.7Atomic¶
In java.util.concurrent.atomic, there are atomic versions for primitive values that give us atomic access to primitives. While less than 32-bit primitives are already atomic by default, these atomic versions also give access to test-and-set, fetch-and-add and compare-and-swap. There is also a weak compare-and-swap, one that may fail spuriously, which may be more efficient if the condition has to be verified in a loop.
One thing we cannot build easily by ourselves are atomic arrays. While it is easy to create an array of atomics, an atomic array has all its content volatile, which gives us volatile semantics for the contents.
volatile int[] x = new int[20];
Normally, when we declare an array, with a volatile in front, the thing we are declaring volatile is the pointer to the array, not the array itself. When the individual elements of the array are accessed, they are not volatile. There is also no way to create an array of volatiles, but atomic arrays fix this issue.
7Memory Consistency¶
In order to be able to write nice, correct concurrent programs, we need to know about memory consistency. This is a really important topic, yet fairly subtle. It is also something that is still being actively researched.
int x = 0, y = 0, a, b; // A perfectly sequential program x = 1; y = 2; b = y; a = x; // We know the result will be (a, b) = (1, 2) // Concurrently however, things are different // Thread 0 x = 1; b = y; // Thread 1 y = 2; a = x; // We get multiple possible results: (a, b) = {(1, 0), (0, 2), (1,2), ... } // However, we cannot get (a, b) = (0, 0)
7.1Write buffering¶
Write buffering is a technique where written data is actually stored in a faster write buffer proper to the processor before being flushed to memory (only when necessary, and in batch). The intent is to save some overhead. On a single processor, the process is entirely invisible. In a multiprocessor context, however, weird things start to happen.
| P0 WB | P1 WB | Memory |
|---|---|---|
x = 1; |
y = 2; |
- |
b = 0; |
a = 0; |
- |
| - | - | x = 1; |
| - | - | y = 2; |
| - | - | a = 0; |
| - | - | b = 0; |
x = 1; is cached in P0's write buffer. If x is to be read again, then the write buffer is checked against before accessing main memory. Meanwhile, P1 can do the same with y = 2;. Then, P0 tries to read y. Seeing it has not written to y, it accesses it from main memory and reads a value of 0. Similarly, P1 reads 0 from x. They then both write respectively to a and b and ultimately flush the results to main memory.
Now we end up with (a, b) = (0, 0) despite the fact it did not make sense when looking at the possible interleavings alone.
7.2Memory Model¶
What we need is a new way to understand how things work. What are the things we could guarantee? What are the conditions under which a thread is allowed to see the writes of other threads?
There are lots of memory model to define what is allowed, and what is not allowed. A multiprocessor by itself has a bare-bone memory model which defines what happens before what at a very level, but software memory models are more clearly defined. One of the major one is called Coherence, but the easiest one is called Strict Consistency.
7.2.1Strict Consistency¶
What this model says is that statements can be interleaved, but they must do exactly as they state. There is no funny ordering (e.g. caused by write buffering) allowed at all.
All we need to do to reason about a concurrent program is to look at the possible interleaving alone. However, what strict consistency allows statements to be fiddled around by being reordered (in a way that is perfectly invisible to us).
// Thread 0 // Thread 1 x = 1; a = 1; y = 2; b = 2; // May get reordered to // Thread 0 // Thread 1 y = 2; b = 2; x = 1; a = 1; // so as to use resources more efficiently
7.2.2Sequential Consistency (SC)¶
Sequential Consistency is basically strict consistency with the property that it just has to appear to be strict, it does not have to be. The instructions appear to execute as if the instructions of each thread are execute in order and interleaved. As long as we cannot tell, fiddling can happen.
Basically, we define some global order on all instructions. We think there is some interleaving we do not know about at first, but ultimately happens.
7.2.3Coherence¶
Coherence says that the global order of sequential consistency does not need to be on all instructions, but rather on a variable by variable basis. Basically, we have a timeline for each variable.
// Thread 0 // Thread 1 x = 0; a = y; x = 1; b = x; y = 2; c = x;
In SC, (b, c) = {(0, 0), (0, 1), (1, 1)}. Something that cannot be seen is (b, c) = (1, 0). For the variable y, a = {0, 2}. In SC, we have to think about the order of the statements.
In coherence, we can choose a = 2, but (b, c) = (0, 0). Each memory location has a defined order. We are getting sequential consistency on a variable by variably basis, not for each statement.
7.2.4Processor Consistency¶
Operations of a single processor are SC.
| Processor0 | Processor1 | Processor2 | Processor3 |
|---|---|---|---|
x = 1; |
x = 3; |
a = x; (1) |
d = x; (3) |
y = 2; |
y = 4; |
b = y; (4) |
e = y; (2) |
| - | - | c = x; (3) |
f = x; (1) |
Whatever Processor2 sees, it has to respect the fact that Processor0 has done x = 1; y = 2; and Processor1 has done x = 3; y = 4;, in these particular orders. Still, what Processor1 does might happen before Processor0 does, or it might be interleaved in some way; it is independent for any processor which looks up the variables.
When Processor2 reads x for a = x;, maybe the value 1 is read. When the value y is read for b = y;, maybe the value 4 is read. Then, when x is read again for c = x;, it must read the value of 3, in order to match an ordering which makes sense.
Processor3 might see a different order; instead of Processor0's actions then Processor1's, it be see the inverse. Still, both Processor2 and Processor3 are agreeing on the inner orderings of Processor0 and Processor1.
We basically have to draw a timeline for each processor (in contrast to each variable with coherence); as long as the reads respect the timelines, everything is good. Notice however that it is not coherent; there is no canonical ordering of each individual variables. P2 sees x = 1; x= 3; whereas P3 sees x = 3; x = 1;.
Nb: Processor consistency and coherence are not comparable. Anything that is sequentially consistent is necessarily coherent and processor consistent. However, things that are coherent are not necessarily processor consistent and vice-versa.

