1Java memory model continued¶
1.1Happens-Before Consistency¶
What we are going to get here is a partial order on thread trace action, and that partial order is going to be per HB edges. So we build a graph of the statements that happen inside a program and we are going to ask ourselves what is its HB consistency, based on that partial ordering that we built inside it.
So we have this graph that has nodes and HB edges that tells us what goes before what. Inside this graph,
a read may see a write. Then we wonder, when we are reading variable x, which of the writes to x is a thread allowed to see inside the program.
A read of x (i.e, R(x)) is allowed to see a write of x (i.e, W(x)), unless:
R(x)happens beforeW(x)(i.e.,R(x)<W(x)in our partial order). We are not allowed to see in the future.- The write to
xhappens before another write toxthat happens before the read ofx(i.e.,W(x)<W'(x)<R(x)).
These 2 rules form the Happens-Before Consistency. Once we build a graph, and we make sure that we check the property (i.e., we do not violate the two rules), the program execution is Happens-Before consistent. Any other possible outcome, as long as we dont violate these two rules, is going to be okay (whatever that means).
1.1.1Example 1¶
int x = 0, y = 0; // Thread 0 // Thread 1 r1 = y; r3 = x; x = 1; y = 1; x = 2; r2 = x;

At each read, we can independently choose any write that we can see. By building such a graph and trying not to violate the two rules of HB consistency, we are trying to solve all the race conditions that could happen in the execution of the program.
1.1.2Example 2 (out-of-thin-air values)¶
int x = 0, y = 0; // Thread 0 // Thread 1 r1 = x; r2 = y; y = r1; x = r2;
Now we can print the result at the end and it prints 42, for both x and y. Now isn't that weird? How can it prints 42 when we have initialized both variables as 0. There must be something broken in the code, right? Let us draw the HB graph:
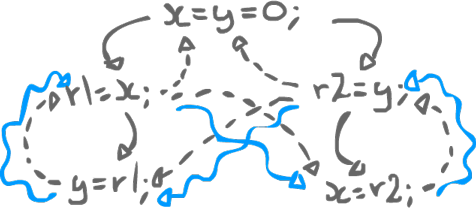
Where did y come from? y came from r1. Where did r1 come from? r1 came from x. Where did x come from? x came from r2. Where did r2 come from? r2 came from y! y comes from y (and x comes from x.)
In this example, we have a causality cycle. Once we have a causality cycle, anything goes. Any value is allowed. This feature is undesirable in any programming language. 42, in our last example, is called an "Out-of-thin-air" value. Where did it come from? There is no 42 in our program. It does not make any sense. It just popped out of thin air. This is obviously undesirable.
This is where a lot of complexity from the Java memory model starts to come into play. It starts off saying: "Okay, so there are these correctly synched program, they are sequentially consistent, they have no data races. For program with data races (like that of the last example), let us build this HB consistency graph and after that we give ourselves the freedom to do whatever we want." And what we end up with is something that can sometimes be pretty weird. So, we have the possibility, if we have some cycles in our HB graph (Causality cyles), to justify any value. If our program prints a random 42, we cannot go to the compiler or VM vendor or hardware vendor (or whoever else) and say "Dude, something is broken inside there." The guy will just say to us that it is perfectly legal, since it does not violate HB consistency.
Bottom line: we want to prevent some of those causality cycles in the HB graph. Obvious solution: prevent all cycles! Unfortunately, some causality cycles are actually okay. Some of them make sense with respect to optimization or things we might do to our program to make it faster.
1.2Allowable cycles¶
int a = 0, b = 0; // Thread 0 // Thread 1 i = a; k = b; j = a; a = k; if (i == j) b = 2;
Is it possible for i == j == k == 2? Seemingly, in order for that to happen, there has to be a cycle as 2 comes from b = 2;. Forbidding causality cycles, this should not happen (even though 2 is not a out-of-thin-air value).
However, b = 2; is independent; we can modify the program by moving it up. Indeed, within Thread0, a does not change, and i == j is always true (it can thus be removed). We end up with the following:
| Thread0 | Thread1 |
|---|---|
b = 2; |
- |
| - | k = b; |
| - | a = k; |
i = a; |
- |
j = i; |
- |
There is no cycle anymore, but i == j == k == 2.
1.3Justification Process¶
So we are not necessarily forbidding cycles, but in order to find out what happens in a program that has data races in it, it has to undergo a justification process, trying to prove what is allowed, and what is not allowed inside a process.
Starting with a well-behaved execution (that is, the execution will only ever see writes that actually do happen before (HB)). Then, we are going over an iterative process:
- Choose a data race. Look at the possible writes it might see.
- Choose to commit a read/write connection (a read must see that write).
- Do this again until there are no more races.
1.3.1Example¶
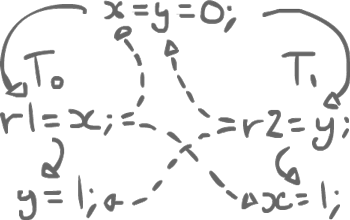
Say x = y = 0;. Thread0 does r1 = x; y = 1; and Thread1 does r2 = y; x = 1;. No synchronization, no volatile variables; there are 2 data races.
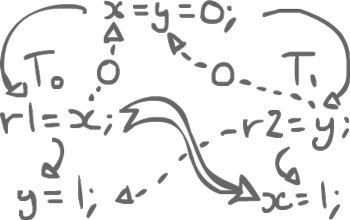
For r1 = x; which must read the value of x, which write can it see? One that happens before, so 0 from its initialization. Same thing for the other thread with y. Still, that does not resolve the race conditions. x or y could receive value 1 from the other thread. As such, we can choose to commit the other write.
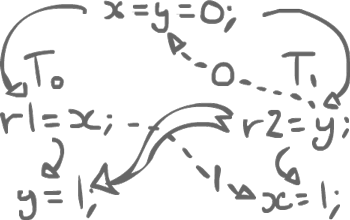
Then, we redo the execution assuming that x rather has the value 1. Now, just as before, we still have a data race for y and we can commit y = 1;.
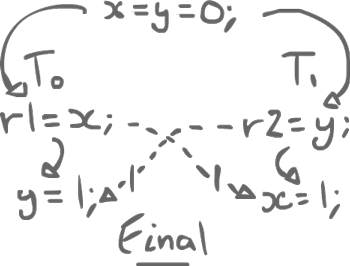
We do not have any race condition anymore. The final values of r1 and r2 are both 1.
Nb: At this stage, the memory model is still broken. We should only write programs that are correctly synchronized, with no data races, with sequential consistency.
1.4A lack of data races¶
A data race is an unordered access by two threads to the same data/memory location, of which at least one is a write.
The ordering, in the case of Java, is our Happens-Before order (HB), which in itself, is the union of the program order with the synchronization order.
Some of that order is very obvious from the program. The synchronization order is a runtime property. In the end, a program being datarace-free (DRF) is actually a runtime property.
x = y = 0; // Thread 0 // Thread 1 do { do { r1 = x; r2 = y; } while (r1 == 0); } while (r2 == 0); y = 42; x = 42
Is this program data race-free? There are two data races, but once the justification process is applied and a real happens-before graph is built up from the actual runtime trace, we end up with a well-behaved execution. As such, we get two infinite loops, making the y = 42; and x = 42; useless, and removing the data races. The program is correctly synchronized, but in a subtle way.

