Last time we talked about memory models, SC, coherence, PC, and about linearization.
x86 -> documentation gives examples of what can or can’t happen
IRIW -> shouldn’t happen
n6 -> observed (but not supposed to be)
n4 -> technically allowed
1Hardware implementation of concurrency¶
1.1x86-TSO¶
Each thread has a FIFO buffer

On intel -> there's an instruction called LOCK (LOCK prefix)
1.1.1Concept of fence¶
After acquiring the lock, the only way to release it is to flush (execute) the write buffer (WB). The lock acts as a fence (can't cross it as long as the buffer isn't flushed).
MFENCE -> (flush -> WB)
(MFENCE is another instruction)
(Check here: http://preshing.com/20120515/memory-reordering-caught-in-the-act/)
If a thread exec Lock instruction
- acquires the lock
- stops every thread from reading from main memory, or even from their own WB
- when it’s done, releases the lock
1.2Set of primitive events¶
Wp[a] = v // thread p writes v to a Rp[a] = v // thread p reads a Fp // fence (you can’t do this micro event until your WB is empty) Lp // lock Up // unlock τp // p commits the oldest write in WBp to main memory (flush action)
1.2.1Example¶
p: INC[0x55]
assume p has in its WB [0x55] = 0
Lp ——————
Rp[0x55] = 0
Wp[0x55] = 1
τ // issue [0x55] = 0
τ // issue [0x55] = 1
Up ——————
1.2.2Rules¶
| Instruction | Description |
|---|---|
| Rp[a] = v | p can read v from [a]. If p is not blocked and the WBp does not contain [a] then get v from main memory |
| Rp[a] = v | p can read v from [a] if p is not blocked, and p has a most recent write of [a] = v in WBp, then get v in WBp |
| Wp[a] = v | p can write v to [a] WBp at any time |
| τp | if p is not blocked it can silently send the oldest write in WBp to main memory |
| Fp | if WBp is empty, p may do Fp |
| Lp | if the lock is not hold by another thread, p can acquire the lock |
| Up | if p holds the lock and WBp is empty |
These rules make sure progress condition is ensured (eventually all the writes are propagated from WB to main memory).
With this model, you can’t get IRIW (independent read independent write) (disallowed).
n6 is allowed (WB justification still holds). n4/n5 is not explicitly disallowed. (n6, n5, n4 and iriw are comma cases of concurrency problems that you'd want to avoid).
| x = 1 | x = 2 |
|---|---|
eax = x(2) |
ebx = x(2) |
Proof
| P0 | P1 |
|---|---|
W0[x] = 1; τ0 (x = 1); R0[x] = 2 |
W1[x] = 2; τ1 (x = 2); R1[x] = 1 |
Either way, τ1 and τ0 have to happen in any order, so R1[x] wouldn’t be 1 (and this situation wouldn’t happen)
2Linux kernel spin lock¶
How it's implemented:
enter(EAX has lock address) start: LOCK: DEC[EAX] JNS enter spin: CMP [EAX], 0 JLE spin JMP start exit: LOCK: MOV[EAX], 1 <— removed lock prefix for optimization
Example:
enter(x) y=1 exit(x) -> with LOCK in the exit -> flush (with x86-TSO)
Without LOCK in the exit, it still works thanks to the fact that we have a nice FIFO order.
3The Java Memory Model¶
The models we have seen so far actually effect what is allowed in concurrent programming. Whenever we are accessing data, we have to know what memory model the system actually provides. In a language like C, historically, there has not been anything about PThreads. The hardware itself provides some kind of memory model. Often, not something theoretically clean like processor consistency, but rather something that is a lot more complicated.
3.1Before Java 1.5¶
Java runs in a Virtual Machine (JVM). That virtual machine is actually a multiprocessor environment, and it has a memory model. Before Java 1.5, we had this huge list of rules.
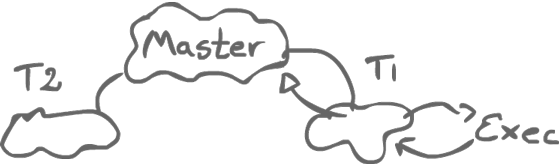
There was some master memory and the individual threads could access the master memory, but also had their own local memory. What if two threads are accessing the same variables? What do they see? Micro-steps of execution would define what was allowed with a big list of rules. The problem was that this was flawed.
There are two tangents for a memory model. We can either get a slow, but understandable memory model which bases itself on sequential consistency, or a fast, but weird memory model which makes it harder to program with.
Now, you might see code that looks like this (where p and q are objects). We are storing p.x and q.x in local variable i, j and k.
// Thread 0 int i = p.x; int j = q.x; int k = p.x;
We can find different optimizations to this code. When we see reading p.x, then reading q.x, then reading p.x again, it is possible that p and q are the same object (same object, different names). That however, is a little hard to be sure of. But one thing we can be sure of, looking at the sequence of code, is that by reading p.x, then q.x, then p.x again, we have not affected anything, except for i, j, and k. So we can actually modify the code as follows:
// Thread 0 int i = p.x; int j = q.x; int k = i;
That might be a faster way of doing things. Now, what could actually happen at run time, is that, maybe p and q really are the same object, and they are being accessed (written to/read) by another thread. So we might have something like:
// Thread 0 // Thread 1 int i = p.x; p.x = 1; // or q.x int j = q.x; int k = i;
p.x (or q.x) is a particular memory location. So imagine we initially saw a 0 in this memory location (int i = 0;). Then we read the same memory location and we saw a 1 (int j = 1;). Then we read the same memory location (from a programmer's perspective, unaware of the optimization made at runtime), and we see a 0 (int k = 0;). What does this mean? Inside here, the system is not coherent.
Coherency says that a particular variable (or memory location) is placed inside memory. Writes should happen in a particular order, but it should not be possible to go backward in time.
As a rule of thumb, coherence is a lower bounds for programmers. If we want to understand what is happening inside a program, if we receive something even weaker than coherence, trying to program inside it and proving the programs actually work becomes extremely tricky.
3.2Revision for 1.5¶
Post 1.5, we want to give a useful programming model for programmers, but we want the flexibility to execute things quickly. The idea is that we are going to divide the world: we are going to reward the good programmers and punish the bad ones. Programs are going to be divided in two classes:
- The Good Programs: Correctly synchronized programs. They do not have data races. The reward: we can assume sequential consistency. The catch: writing data race-free programs is a tricky thing to do.
- The Bad Programs: Incorrectly synchronized programs. They contain data races.
3.2.1Semantics for incorrectly synchronized programs¶
(Happens-before: http://preshing.com/20130702/the-happens-before-relation/)
The core idea is the Happens-Before Consistency, a very straightforward model. We are going to think of all the runtime actions of threads as nodes of a graph. The edges of the graph will express the Happens-Before consistency relation. This mechanism will express what is allowed, or rather, what HAS to be true inside the program (what has to happen before what). We will put an edge from a to b if a must happen before b. So we will want to list all the runtime actions, draw this big graph where each node represents a runtime action and start drawing edges between these nodes.
3.2.1.1Happens-Before Edges¶
There are two types of edges in a HB graph. The intra-thread actions edges, and the edges between threads.
- Intra-thread actions
- These are the easy ones to do. If you have a single a thread, and this thread does (in terms of action):
a; b; c; d;.
In the graph, we have a -> b -> c -> d. So we know that a happened before b, b happened before c, and c happened before d. So in a sense, intra-thread actions are totally boring.
What we are concerned about here, is not the behavior of a single thread, but the behavior of the program as a whole. We are interested in what happens between threads, that is, the edges between different threads.
- Edges between threads
- We are going to put an edge between different threads actions:
1) from an unlock on monitor/object m to all subsequent locks on m.
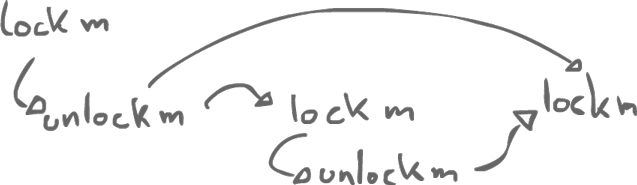
What we got here is a trace: we see what actually happens. So we have our regular program order and we have also have a synchronization order.
- Synchronization order
- Runtime ordering of synchronization operations (locks and unlocks). We look at all the synchronization actions inside our program and we compute a total order on them and this gives us our synchronization order.
2) from each write of a volatile variable v to all subsequent reads of v
Volatile reads and writes are also considered synchronization operations, so they also participate to the synchronization order.
volatile int v; // Thread 0 v = 2; // Thread 1 a = v;
At runtime, one of these two actions happens before the other one.
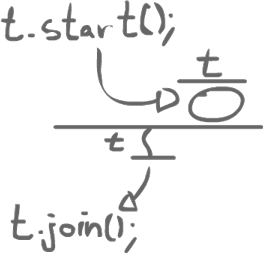
There are also a few other rules for happens-before. For example, the first action of a thread that we start comes after the prior thread which created it. A join also happens after then end of a thread.

