Wikinotes

Maintainer: admin

Annotations for the notes created by Professor William J Anderson for his fall 2011 class. Based on revision 11, last updated November 28, 2011. Includes more detailed explanations, further examples, and possibly other stuff too.

$$P(A) = \frac{70}{360} \approx 0.19; \quad P(B)= \frac{279.5000 - 145.6678}{360} \approx 0.37; \quad P(C) = 0$$

although the answer for C depends on the assumed precision; if we take 45.7 as meaning anything between 45.65 (inclusive) and 45.75 (exclusive), then the probability of C would become 0.00027 instead. But that's just being me being pedantic.

$P (A \cup B) = P (A) + P (B) − P (A \cap B)$ is an important formula, but it doesn't need to be memorised, as just drawing out the Venn diagram shows clearly why it is correct. Finding the union of $P(A)$ and $P(A^c)$ (that is, the probability of an event and the probability of its complement) does not require paying attention to the intersection of the two events because there is no intersection. (In other words, they are disjoint.)

The example can be more easily (and possibly more intuitively) solved without listing the sample spaces. For (1), consider that there are exactly 3 red fish out of five fish total, so the probability of getting a red fish the first time is $\frac{3}{5}$. Since you're not putting the fish back in the tank afterwards (poor fish ... one can only hope they've moved on to greener pastures), the number of fish remaining after the first "draw" is 4, with only two of them being red (since you've just taken one of the red brethren out). The probability of getting a blue fish on your second draw is thus $\frac{2}{4}$. The probability of this event following the first is the product of the two, so $\frac{3}{5} \times \frac{2}{4} = \frac{6}{20} = 0.3$.

For (2), the probability is also $0.3$ because the probability of getting a red fish on your second draw is also $\frac{2}{4}$.

For (3), you can add up the separate probabilities of getting a red fish then a blue fish and getting a blue fish then a red fish. For the latter, the probability is $\frac{2}{5} \times \frac{3}{4}$ which is of course equal to $0.3$. The former is also $0.3$. So the total probability of getting one red fish and one blue fish is $0.6$.

For (1), there are five choices for the first character of the word. For the second character, there are only four letters we can choose from, and for the third, there are only three, and so the answer is undoubtedly $5 \times 4 \times 3 = 60$. For (2), the number of choices for each character remains five, so the answer is $5^3 = 125$.

Instead of thinking of $P^n_r$ being defined like this:

$$P^n_r = \frac{n!}{(n-r)!}$$

you could alternatively think of it as $n \times (n-1) \times (n-2) \times ...$, with $r$ terms total. The former is obviously correct as well, and more mathematically precise, but I find it hard to think about it that way. Your mileage may vary of course.

I can't think of a good alternative way for interpreting the formula for combinations, so the one given will have to do I guess. Essentially, you're finding the number of permutations, then ignoring the permutations that are just a different ordering of a previous one (because order doesn't matter in combinations). This can be done by dividing the first formula by the factorial of the number of things you don't have room for (if you use the analogy that 9 choose 4 means you have 9 things, and you only have room for 4, so there are 5 things you don't have room for). But this isn't very useful, so.

The solution provided in the notes for this confused me for a while, until I figured out what was going on. One of the tires chosen has to be the one ranked third among the 8, so that only 3 spots remain to be filled with tires. Those three must be chosen from those ranked 4, 5, 6, 8, and 8, as choosing tires ranked 1 or 2 would threaten 3's temporary feeling of superiority. So out of 5 tires, we choose 3. So the answer is $C^5_3 = \frac{5 \times 4}{2} = 10$.

(1) evaluates to $\frac{60}{126} = \frac{10}{21} \approx 0.476$, for those wondering. (2) can also be solved by finding the probability, at any turn, that a peach will be chosen: $\frac{5}{9} \times \frac{4}{8} \times \frac{3}{7} \times \frac{2}{6} \times \frac{1}{5} = \frac{1}{126}$. For (3), the possibilities are: 3 peaches and 2 bananas; 4 peaches and one banana; and 5 peaches and no bananas. So just find the probability for each (we already figured out two of the three; the remaining one can be calculated in the same manner as (1)) and add them all up. Evaluates to $\frac{60}{126} + \frac{1}{126} + \frac{20}{126} = \frac{81}{126} = \frac{9}{14} \approx 0.643$.

I don't know why the solution for (1) has a random "51" next to the $C^8_3$ part. What is it doing there? What does it mean? Is there something important that I am missing? In any case, this one can be solved by noticing that one taxi being sent to airport C conveniently removes that airport from the list of possibilities, as C only really wanted one taxi anyway. So there are 8 taxis that you want to send to either A or B. A needs 3, so the number of ways you can send 3 taxis to airport 8 is $C^8_3=56$ (which is incidentally equal to $C^8_5$, which is what you might have gone with had you thought of it from the perspective of airport B, although people rarely do).

For (2), we see that once again airport C is conveniently filled, making this a simple binary situation. There are 3 airports and 3 taxis that need to be repaired, and there are $3 \times 2 \times 1 = 6$ ways of mapping one taxi to each airport (basically, sampling without replacement). For each of these ways, there are 6 other taxis that need to be sent to one of two airports, with airport A only needing 2 more. So the answer is $6 \times C^6_2 = 6 \times 15 = 90$. Not sure what the unexpected "41" is doing here, either.

Important formula. Don't forget it lol. Easy enough to arrive at independently, though.

For the first example (where A is the event of getting sum of 5, and B that the first die is less than or equal to 2), we could have alternatively found the number of situations where both of them are true ($\{(1, 4), (2, 3)\}$, so 2) and found the number of situations where the latter is true ($6 + 6$ so 12), resulting in $\frac{2}{12}$. This is an equivalent but perhaps more approach to solving the problem.

So this is basically what I wrote about our first visit to this fishtank, rendering what I wrote useless, but whatever, I've already written it, not going to delete it now.

If A is the event that the second card drawn is an ace, and B is the event that the first card drawn is not an ace, then $P(A \cap B) = \frac{50}{52} \times \frac{4}{51}$ (since they're independent, and since there are 4 aces in a deck, which I must say is surprisingly easy to forget) and $P(B) = \frac{50}{52}$ so $\frac{P(A \cap B)}{P(B)} = \frac{4}{51}$ It took me a moment to remember how many cards were in a standard deck (I actually had to look it up to be sure) but in hindsight, of course it's 52 - 4 suits, and ace-king means 13 cards per suit, so yeah. The answer implies that there are no jokers in a "standard" deck, because otherwise it would be $\frac{4}{53}$.

What is a slip? I'd love to know.

The first two definitions of independence (proposition 1.3.2) simply says that the happening of one event does not affect the other one. This matches very well with the fact that events are, in fact, considered to be independent.

For (ii), we could have used the complement of the given event as well - the probability that no one will pass is $(1- 0.7) \times (1-0.6) = 0.3 \times 0.4 = 0.12$ so the probability that at least one will pass is $1 - 0.12 = 0.88$. There's often More Than One Way To Do It, something that contributes to the fun of probability.²

I personally make a point of not memorising the formula, and instead think through the problem and figure out the answer based on the possible situations, sometimes using numbers out of 100 (or 1000 or whatever) instead of percentages if that helps. I find it easier that way because then instead of mindlessly plugging numbers into a formula (which can be prone to incorrect recall or usage) I get a feel for what is actually going on and what is being asked. For the Canadian bridge problem, for example, 1% of the bridges are collapsed bridges built by firm 1, and 19% are collapsed, so the answer is logically $\frac{1}{19}$.

This definition is sort of neglected, being shoved in at the end of a section that it doesn't completely belong in and not being furnished with any examples. So I'll give one. There are 10 people in a club, and we want to choose 3 of them to be the chairs. This is a completely egalitarian club so we want to make sure that each person has the same shot at becoming a chair. Each person clearly has a $3/10$ chance of being on the committee, but what about each possible combination of 3 people? Well, since there are $C^{10}_3$ different combinations, each one has a $\frac{1}{C^{10}_3} = \frac{1}{120}$ probability of being the chairs. On second thought, that was a pretty useless example; I kind of see why Anderson didn't add one in the first place.

In the example, it says that the expected value for the constant variable is $E(X) = c$. So the only possible outcome is getting a 5, and all other outcomes are impossible, the expected value would be 5. And so on.

Expected value of the discrete rv $X$: sum of the value times the probability of getting that value for each discrete value ($\displaystyle E(X) = \sum_{x \in R_x} x P(X = x)$)
Expected value of a function $f(x)$: same as above, just substitute the first $x$ with $f(x)$ (so $\displaystyle E(X^3) = \sum_{x \in R_X} x^3 P(X = x)$)
Sum of two functions: sum of the expected values ($E(f(x) + g(x)) = E(f(x)) + E(g(x))$)
A function times a constant: constant times the expected value of the function ($E(cf(x)) = cE(f(x))$)

Very important. Usually the second version of the formula ($E(X^2) - \mu^2$, where $\mu$ is the mean) is easier to use, but sometimes the first version ($E((X-\mu)^2)$) is more appropriate, so make sure to keep both in mind. To show that the second version is equivalent to the first, just multiply it out.

Again important - $P(X = x) = C^n_x p^x q^{n-x}$ where $x$ indicates the number of successes there are, with the probability of success given by $p$. In the edge cases, the probability of getting all successes is $p^n$, as expected, and the probability of getting all failures is $q^n$, which makes sense so all is well in the universe.

The above was just the binomial formula. For distributions following this formula, the expected value is $np$ (so the number of things times the probability of success) and the variance is $npq$ (so the expected value times the probability of failure). The proofs for these are kind of long and involve a lot of factorials. Also, the tables in the back of the book aren't really necessary if you have a calculator, but if you don't, make use of them over trying to compute them by hand.

The provided answers for (1) and (2) are pretty straightforward, so no comments on those. For (3), if you want to solve it the table-less, manlier way:

$$\begin{align*}P(3 \leq X \leq 5) & = P(X = 3) + P(X = 4) + P(X = 5) \\ & = (C^7_3 0.2^3 0.8^4) + (C^7_4 0.2^4 0.8^3) + (C^7_5 0.2^5 0.8^2) \\ & \approx 0.1477 \end{align*}$$

which, incidentally, tells us that the probability of more than 5 holes striking oil is very unlikely indeed, as $P(X \leq 2) + P(3 \leq X \leq 5) = P(X \leq 5)$ is nearly 1.

To find $n$ such that $P(X \geq 1) \geq 0.9$, consider that $P(X \geq 1) = 1 - P(X = 0) = 1 - q^n = 1 - 0.8^n$. So solving for $n$ in $0.8^n \leq 0.1$ gives us $n \geq 11$, so we would need at least 11 holes.

Same as binomial, except you don't have a fixed number of trials and instead keep going until you succeed. Which is a good attitude in general, when it comes to it. The probability of getting a success on the $x$th trial is just the probability of getting a failure on the first trial times the probability of getting a failure on the second trial ... times the probability of getting a success on the last trial (assuming $x > 2). So just $q^{x-1}p$, which is much easier to write than the above.

The expected value is given by $\frac{1}{p}$ (I don't really get the proof) and the variance is given by $\frac{q}{p^2}$.

This means that the probability of getting a success after trial $m + n$ given that you've gotten a success after trial $m$ is the same as the probability of getting a success after trial $n$. For instance, if Alice keeps buying lottery tickets until she wins something, and the probability of winning something is 0.1, then the probability of her taking more than 3 purchases to win something ($P(B)$) is found as follows:

$$\begin{align*} P(X > 3) & = 1 - (P(X = 1) + P(X = 2) + P(X = 3)) \\ & = 1 - (0.1 + 0.9 \cdot 0.1 + 0.9 \cdot 0.1^2) \\ & = 1 - 0.1 \sum_{i = 0}^{i-1} 0.9^i \\ & = 1 - 0.271 \\ & = 0.729 \end{align*}$$

and the probability of her taking more than four purchases to win something ($P(A)$) is the above minus $P(X = 4)$, so $P(A) = 0.729 - 0.1 \cdot 0.9^3 = 0.6561$. The conditional probability of her taking more than 4 purchases given that she has taken more than 4 is given by:

$$\frac{P(A \cap B)}{P(B)} = \frac{P(A)}{P(B)} = 0.9$$

The probability of her taking more than one purchase to win something, on the other hand, is given by $P(X > 1) = 1 - P(X = 1) = 1 - 0.1 = 0.9$. Which is, happily, the same as the result above.

This is the general case of which the geometric distribution was merely a specific case (so instead of stopping after 1 success, we stop after $r$ successes). The probability function is given by

$$P(X = x) = C^{x-1}_{r-1} p^r q^{x-r}$$

where $x \geq r$ is the trial on which the $r^th$ success was observed. This formula is derived kind of recursively, which is pretty weird when you think about it but I guess it makes sense.

The expected value is $\frac{r}{p}$ and the variance is $\frac{rq}{p^2}$ (derived later, using moment-generating functions).

This is similar to the binomial distribution, except $p$ and $q$ change due to it being "without replacement". The formula is

$$P(X = x) = \frac{C^r_x C^{N-r}_{n-x}}{C^N_n}$$

where $x$ is the number of red balls in a sample, $n$ is the size of the sample, $N$ is the number of balls total, and $r$ is the number of red balls total.

The expected value is $\displaystyle \frac{nr}{n}$ and the variance is $\displaystyle n\frac{r}{N} \frac{N-r}{N} \frac{N-n}{N-1}$.

Used when you know events occur at an average rate, or something. The probability function looks like this:

$$P(X = x) = \frac{\lambda ^x e^{-x}}{x!}$$

The expected value and variance are both $\lambda$, which is convenient.

Apparently the Poisson distribution and the binomial distribution are related, in that the probability $P(X = x)$ for a binomial distribution converges to the function given above as $n \to infty$ and $p \to 0$ (with $\lambda = np$ remaining constant). This means that for large values of $n$ and small values of $p$, we can approximate $P(X = x)$ using the Poisson distribution formula. Ideally, $np \leq 7$ (for a better approximation).

Still not really sure what the point of these things is, but I hear through the grapevine that the moment generating function uniquely determines the distribution.

Okay, this seems to clear it up: moments are things like $E(X)$, $E(X^2)$, $E(X^n)$ etc. Moment generating functions simply provide an easier way of finding the values for these moments, which is useful if we want to know the mean or the variance.

Since $M^{(n)}(0) = E(X^n)$, we just have to find the first derivative of the moment generating function at $x = 0$ to find $E(X)$, the second derivative to find $E(X^2)$, and so on.

$$M(t) = E(e^{tX}) = \sum_{x \in R_X} e^{tx} P(X = x)$$

where $M(t)$ is the moment generating function and $R_X$ is the possible values of $x$ I suppose.

Incidentally, $\displaystyle M(t) = \sum_{n=0}^{\infty} \frac{\mu'_n t^n}{n!}$.

Binomial distribution: $\displaystyle M(t) = \sum_{x=0}^n e^{tx} C^n_x p^x q^{n-x} = (pe^t + q)^n$
Geometric distribution: $\displaystyle M(t) = \sum_{x = 1}^{\infty} e^{tx} p q^{x-1} = \frac{pe^t}{1 - qe^t}$
Poisson distribution: $\displaystyle M(t) = \sum_{x = 0}^{\infty} e^{tx} \frac{\lambda^x e^{-\lambda}}{x!} = e^{-\lambda(1-e^t)}$

The distribution function differs from the probability function in that where the latter was concerned with $P(X = x)$, the former deals with $P(X \leq x)$. In other words, a cumulative probability function. The terminology is kind of confusing because it's not completely standardised, but in this class we use "distribution function" to refer to the cumulatuve distribution function and probability function to refer to just the $P(X = x)$ thing.

These functions are always nondecreasing, starting from 0 at $- \infty$ converging to 1 at $\infty$

The distribution function is found by integrating the density function, where the density function is just the function that gives the probability of $x$, if that makes sense. (This is sort of misleading since the probability $P(X = x)$ is always 0 for a specific $x$, but I can't find a better way to phrase it.) The integral of the density function over the entire domain is of course equal to 1.

To find the probability that x falls between the real values $a$ and $b$, we simply find the definite integral of the probability density function with those points as the endpoints:

$$P(a \leq X \leq b) = \int_a^b f(x) \,dx$$

where the $\leq$s can be replaced by $<$ if so desired.

To find the expected value, just replace the summation for discrete random variables with an integration:

$$E(X) = \int_{-\infty}^{\infty} x f(x) \,dx$$

To find the expected value of a function (i.e. with $g(X)$ instead of $X$), just replace $X$ with $g(x)$:

$$E(g(X)) = \int_{-\infty}^{\infty} g(x) f(x) \,dx$$

The same things with scalar multiples and addition for discrete rvs apply.³

Variance is fairly straightforward, just replace $g(x)$ with $(x - \mu)^2$ and there you go.

Again, just replace the summation with an integration:

$$M^{(n)}(t) = \int_{-\infty}^{\infty} x^n e^{tx} f(x)\,dx$$

so $E(X)$ is the first derivative, $E(X^2)$ is the second derivative, etc.

Probability density function

$$f(x) = \begin{cases} 0 & \text{ if } -\infty < x < a, \\ \frac{1}{b-a} & \text{ if } a \leq x \leq b, \\ 0 & \text{ if } b < x < \infty \end{cases}$$

So it's equiprobable between the endpoints of $a$ and $b$. Looks like this:

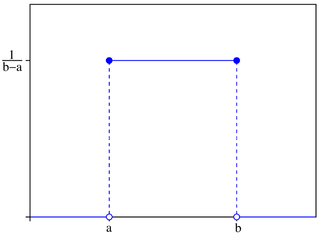
Expected value: $\displaystyle E(X) = \frac{a+b}{2}$ (the midpoint of a and a)

Variance: $\displaystyle Var(X) = \frac{(b-a)^2)}{12}$

Cumulative distribution function:

$$F(x) = \begin{cases} 0 & \text{ if } x < a, \\ \frac{x-a}{b-a} & \text{ if } a \leq x \leq b, \\ 1 & \text{ if } x > b. \end{cases}$$

To find the probability that $x$ will fall between $c$ and $d$, just find the distance between the two that is also between $a$ and $b$, and divide that by the distance between $a$ and $b$. So if $c < a$ and $d > b$, then the probability is obviously 1.

The moment generating function is:

$$M(t) = \frac{e^{tb} - e^{ta}}{t(b-a)}$$

$$f(x) = \begin{cases} 0 & \text{ if } x \leq 0,\\ \frac{1}{\beta}e^{-x/\beta} & \text{ if } x > 0, \end{cases}$$

Expected value: $E(X) = \beta$

Variance: $E(X) = \beta^2$

Cumulative distribution function:

$$F(x) = \begin{cases} 0 & \text{ if } x < 0,\\ 1 - e^{-x/\beta} \text{ if } x \geq 0 \end{cases}$$

Moment generating function:

$$M(t) = \frac{1}{1 - \beta t}$$

Like the geometric distribution, the exponential distribution is "memoryless". In fact, any memoryless continuous random variable has the exponential distribution, which can be thought of as the continuous version of the geometric distribution.

$$\Gamma(\alpha) = \int_0^{\infty} x^{\alpha-1} e^{-x} \,dx, \quad \alpha > 0$$

This function has the following properties:

$0 < \Gamma(\alpha) < \infty$ for all $\alpha > 0$
$\Gamma(1) = 1$
$\Gamma(\alpha + 1) = \alpha\Gamma(\alpha)$, $\alpha > 0$
$\Gamma(n + 1) = n!$
$\Gamma(\frac{1}{2}) = \sqrt{\pi}$

The probability density function is:

$$f(x) = \begin{cases} 0 & \text{ if } x \leq 0, \\ \frac{1}{\Gamma(\alpha) \beta^{\alpha}} x^{\alpha-1} e^{-x/\beta} & \text{ if } x > 0, \end{cases}$$

where $\alpha, \beta > 0$.

Expected value: $E(X) = \alpha \beta$

Variance: $E(X^2) = \alpha \beta^2$

Moment generating function:

$$M(t) = \frac{1}{(1-\beta t)^{\alpha}}$$

where $t < \frac{1}{\beta}$, not sure why.

$$f(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} e^{-\frac{1}{2} \frac{(x - \mu)^2}{\sigma^2}}, \quad -\infty < x < \infty$$

where $\mu$ and $\sigma^2$ are the mean and variance, respectively. It can also be written with $\sigma$ instead of $\sigma^2$ (and some changes to the formula to make it equivalent).

This produces a bell curve centered around the mean, and with a concavity dependent on the value of the variance:

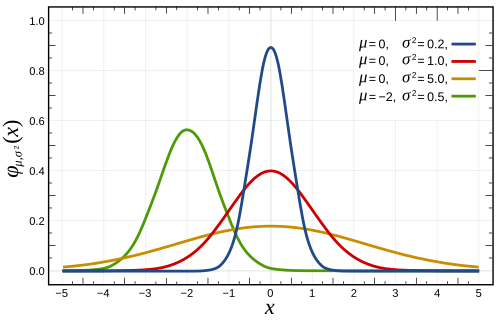
The standard normal distribution is when $\mu = 0$ and $\sigma^2=1$. There will be two tables - one for $P(X > x)$, the other for $P(0 \leq X \leq x)$ - at the end of the exam that can be used as reference. It should be easy enough to use; just remember that $P(Z > z)$ is the same as $P(Z < -z)$ if $\mu = 0$ (and if $\mu$ is not just use that as the center instead of 0).

Page 37, last example:

$P(0 \leq Z \leq 1.4) = 0.4192$
$P(0 \leq Z \leq 1.42) = 0.4222$
$P(Z > 1.42) = 0.5 - (0 \leq Z \leq 1.42) = 0.0788$ (could also have been looked up in the table; this method simply used the fact that the probability on each side of the mean is 0.5)
$P(Z < -1.42) = P(Z > 1.42) = 0.0788$
$P(-1.5 < Z < 1.42) = P(-1.5 < Z < 0) + P(0 < Z < 1.42) = P(0 > Z > 1.5) + P(0 > Z > 1.42) = 0.4332 + 0.4222 = 0.8554$ (not sure why this is the only one with an answer provided - maybe because it's used below)
7 $P(1.25 < Z < 1.42) = 0.5 - P(Z > 1.42) - P(0 < Z < 1.25) = 0.5 - 0.0788 - 0.3944 = 0.0268$

Page 38, first example:

$P(Z > z) = 0.05 \to z \approx 1.645$ (somewhere between 1.64 and 1.65, according to the table)
$P(Z > z) = 0.025 \to z = 1.96$

Page 38, second example:

To do this type of problem, change the endpoints in $P(a < X < b)$ to $P(a - \mu < X - \mu < b - \mu)$ (so subtract $\mu$ from all three sections) and then divide each part by the square root of the variance to find the corresponding endpoints to look up in the standard normal distribution table.

The probability density function is as follows:

$$f(x) = \begin{cases} \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)} x^{\alpha - 1} (1-x)^{\beta - 1}, & \text{ if } 0 < x < 1,\\ 0 & \text{ otherwise} \end{cases}$$

where $\alpha, \beta > 0$

Expected value: $\displaystyle E(X) = \frac{\alpha}{\alpha + \beta}$

Variance: $\displaystyle Var(X) = \frac{\alpha \beta}{(\alpha + \beta)^2 (\alpha + \beta + 1)}$

The moment generating function cannot be obtained in closed form.^?

The probability density function is as follows:

$$f(x) = \frac{1}{\pi} \cdot \frac{1}{1 + x^2}, \quad -\infty < x < \infty$$

There is no expected value or variance for this distribution, which feels oddly unsettling.

However, if we limit the domain to $x \geq 0$, then the expected value is just $\infty$ (although that might require multiplying the standard equation by 2?).

Given a probability distribution where $x$ cannot be negative (i.e. $P(X \geq 0) = 1$), we have the following inequality:

$$P(X > \epsilon) \leq \frac{E(X)}{\epsilon}$$

where $\epsilon > 0$. This works for both discrete and continuous random variables, and can be proven using the properties of definite integration in the latter case.

(Also spelled Chebyshev, Tchebycheff, etc.)

For a random variable with a mean of $\mu$ and a variance of $\sigma^2$, the following inequality holds:

$$P(|X - \mu| > \epsilon) \leq \frac{\sigma^2}{\epsilon^2}$$

for any $\epsilon > 0$.

If the variance is 0, then Chebychev's inequality (and by, well, common sense) then $P(X = \mu) = 1$ (so it's always the mean).

Called joint density functions (jdfs). The same idea as a regular probability density function but extended to 3-dimensional space. There are also joint (cumulative) distribution functions (called JDFs, lol).

Instead of single integrals, we have double integrals, etc.

The marginals are essentially what would be written in the margins of a joint probability function table, as a result of adding up all the values in that particular row or column.

In the continuous case, to find the marginal for $y_1$, integrate with respect to $y_2$:

$$f_1(y_1) = \int f(y_1, y_2) \,dy_2$$

and vice versa.

Covariance is just the bivariate analog of variance, and is given by the formula

$$Cov(X, Y) = E(XY) - E(X)E(Y)$$

If two variables are independent, then their covariance is 0 (but the converse is not true - two variables with a covariance of 0 may still be dependent; check that they satisfy the formula in section 4.3.

First mentioned in the notes in section 4.6 but there's a problem in this section that uses it so whatever.

The correlation coefficient is a measurement of how two variables are related, and is given by the covariance divided by the product of the standard deviations of each variable. Mathematically:

$$\rho_{XY} = \frac{Cov(X, Y)}{\sigma_X \sigma_Y}$$

where $\sigma$ is the square root of the variance, $\sigma^2$.

$$f_{12}(y_1|y_2) = P(Y_1 = y_1 | Y_2 = y_2) = \frac{P(Y_1 = y_1, Y_2 = y_2}{P(Y_2 = y_2)} = \frac{f(y_1, y_2)}{f_2(y_2)}$$

for both probability density and probability distribution functions.

The conditional expectation is just the integral of the product of the above function and the $g(x)$ part of $E(g(x))$.

$$f(y_1, y_2) = f_1(y_1) \cdot f_2(y_2)$$

where the functions are all density functions and

$$F(y_1, y_2) = F_1(y_1) \cdot F_2(y_2)$$

where the functions are all distribution functions.

$Cov(X, Y+Z) = Cov(X, Y) + Cov(X, Z)$
$Cov(aX, bY) = abCov(X, Y)$
$Cov(X-Y, X + Y) = Cov(X, X+Y) + Cov(-X, X+Y) = Cov(X, X) + Cov(X, Y) + Cov(-X, X) + Cov(-X, Y)$
$= Var(X) + Cov(X, Y) - Var(X) - Cov(X, Y) = 0$ ^{I think}

For (2), you know that $Cov(X, Y)$ and $Cov(Y, X)$ (equivalent, incidentally) are 0 because the variables X and Y are stated to be independent. lol.

$$P(X_1 = x_1, \ldots, X_k = x_k) = \frac{n!}{x_1! \ldots x_k!} p_1^{x_1} \ldots p_k^{x_k}$$

where all the $x$'s are natural numbers and their sum is $n$.

$M_X(0) = 1$
$M_{aX + b}(t) = e^{tb} M_X(at)$
$E(X^n) = M^{(n)}_X(0)$
Distributions with the same moment generating function are equivalent
If $X = X_1 + \ldots + X_n$, then $M_X(t) = M_{X_1}(t) \cdot ... \cdot M_{X_n}(t)$.

This section will not be on the exam, so, fuck it

I wonder if it's possible to actually choose a fruit out of this box randomly, since bananas and peaches don't exactly have the same shape. ↩
But not Perl. ↩
As integration is closed under scalar multiplication and addition? Not really? Sort of? ↩

Annotations for Anderson's notes

1Introduction and definitions¶

1.1Basic definitions¶

1.1.1On spinning a spinner¶

1.1.2On the rules for computing probabilities¶

1.1.3On tanks full of coloured fish¶

1.2Permutations and combinations¶

1.2.1On three-letter words¶

1.2.2On permutations¶

1.2.3On combinations¶

1.2.4On choosing a mediocre tire¶

1.2.5On randomly choosing fruits from a fruit box1¶

1.2.6On repair-needing taxis and taxi-needing airports¶

1.3Conditional probability and independence¶

1.3.1On the definition of conditional probability¶

1.3.2On rolling dice¶

1.3.3On the tank of coloured fish, revisited¶

1.3.4On aces and drawing cards from a deck¶

1.3.5On slips¶

1.3.6On independence¶

1.3.7On Susan and Georges¶

1.4Bayes' rule and the law of total probability¶

1.4.1On the formula for Bayes' rule and dangerous Canadian bridges¶

1.4.2On random sampling¶

2Discrete random variables¶

2.1Basic definitions¶

2.1.1On constant random variables¶

2.1.2On the expected value of discrete functions¶

2.1.3On variance¶

2.2Special discrete distributions¶

2.2.1The binomial distribution¶

2.2.1.1On the formula for Bernoulli trials¶

2.2.1.2On Northern Quebec getting drilled¶

2.2.2The geometric distribution¶

2.2.2.1On the definition of a geometric distribution¶

2.2.2.2On the memoryless property of geometric distributions¶

2.2.3The negative binomial distribution¶

2.2.3.1On the definition of a negative binomial¶

2.2.4The hypergeometric distribution¶

2.2.4.1On the definition of a hypergeometric distribution¶

2.2.5The Poisson distribution¶

2.2.5.1On the definition of the Poisson distribution¶

2.2.5.2On the relation between Poisson and binomial¶

2.3Moment generating functions¶

2.3.1On the significance of moment generating functions¶

2.3.1.1On finding the moment generating function of a distribution¶

2.3.1.2On the moment generating functions of specific distributions¶

3Continuous random variables¶

3.1Distribution functions¶

3.1.1On the definition of distribution functions¶

3.2Continuous random variables¶

3.2.1On distribution and density functions for continuous random variables¶

3.2.2On expected values and variance for continuous random variables¶

3.2.3On moment generating functions for continuous random variables¶

3.3Special continuous distributions¶

3.3.1The uniform distribution¶

3.3.1.1On the definition of the uniform distribution¶

3.3.2The exponential distribution¶

3.3.2.1On the definition of the exponential distribution¶

3.3.2.2On the memoryless propety of the exponential distribution¶

3.3.3The gamma distribution¶

3.3.3.1On the definition of the gamma function¶

3.3.3.2On the properties of the gamma distribution¶

3.3.4The normal distribution¶

3.3.4.1On the definition of the normal distribution¶

3.3.4.2On the example probabilities using the standard normal distribution¶

3.3.5The beta distribution¶

3.3.5.1On the definition of the beta distribution¶

3.3.6The Cauchy distribution¶

3.4Chebychev's inequality¶

3.4.1On Markov's inequality¶

3.4.2On Chebychev's inequality¶

4Multivariable distributions¶

4.1Definitions¶

4.1.1On joint probability functions¶

4.1.2Marginal and conditional distributions¶

4.1.2.1On the significance of marginal probabilities¶

4.1.3On covariance¶

4.1.4On the correlation coefficient¶

4.1.5On the conditional probability function¶