Will eventually include a review of absolutely everything in the entire course. Sources: Professor Anderson's notes on WebCT, and the Mathematical Statistics with Applications textbook by Wackerley, Mendenhall, and Scheaffer.
Stuff to cover:
- Lecture notes (everything except stuff marked with a †)
- The following sections from Mathematical Statistics with Applications:
- 6.7
- 7.2
- Chapter 8
- 9.1-9.7 plus exercise 9.8
- Chapter 10
- 11.1-11.7
- 13.1-13.6, 13.8-13.9
- 14.1-14.4
Problems from the assignments will be covered in the HTSEFP, and things that we need to memorise can be found on the Formulas to memorise page.
Under construction
- 1 Sampling distributions
- 1.1 The basic distributions
- 1.2 Applications of some distributions
- 1.2.1 Sample mean and variance
- 1.2.1.1 Expected value of the sample mean
- 1.2.1.2 Variance of the sample mean
- 1.2.1.3 Relation to the normal distribution
- 1.2.1.4 Expected value of the sample variance
- 1.2.1.5 Correlation between the sample mean and the individual samples
- 1.2.1.6 Independence of the sample mean and sample variance
- 1.2.1.7 Relation to the chi square distribution
- 1.2.1.8 Relation to the t distribution
- 1.2.1 Sample mean and variance
- 1.3 Order statistics
- 2 Estimation
- 3 Confidence intervals
- 4 Theory of hypothesis testing
- 5 Applications of hypothesis testing
- 6 Linear models
- 7 Chi-square tests
- 8 Non-parametric methods of inference
1Sampling distributions¶
Chapter 7 in the textbook, section 1 in Anderson's notes.
1.1The basic distributions¶
1.1.1The chi-square distribution¶
Density function
The density function of a random variable $X$ with a chi-square distribution with $n$ degrees of freedom ($X \sim \chi^2_n$, $n \geq 1$) is as follows:
$$f(x) = \begin{cases} \frac{1}{2^{n/2}\Gamma(n/2)} x^{(n/2)-1}e^{-x/2} & \text{if }x > 0, \\ 0 & \text{otherwise}\end{cases}$$
Graph
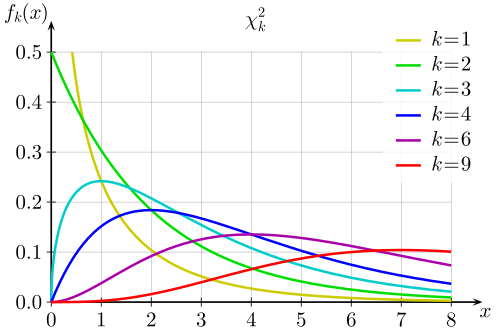
Properties
Incidentally, this is a special case of the gamma distribution, with $\alpha = n/2$ and $\beta = 2$. We can consequently derive the distribution's expected value, variance, and moment-generating function:
$$\begin{align*}E(x) & = n \\ Var(X) & = 2n \\ M_X(t) & = \frac{1}{(1-2t)^{n/2}}\end{align*}$$
Relation to other distributions
- Using the central limit theorem, we can map a chi-square distribution, $X$, to the normal distribution with mean 0 and variance 1 ($N(0, 1)$), by the following formula:
$$\frac{X-n}{\sqrt{2n}}$$
- The sum of independent chi-square random variables has a chi-square distribution. Its number of degrees of freedom is equal to the sum of the d.f. of the random variables. Or, in mathematical terms, if $X = X_1 + \ldots X_m$ where $X_i$ is an independent chi-square random variable with $n_i$ degrees of freedom, then $X \sim \chi^2_n$ where $n = n_1 + \ldots + n_m$. Proof of this is accomplished by writing out the moment-generating functions. (Note that this also implies that if $X$ is the sum of two chi-square distributions, and we know the d.f. of $X$ and of one of the other distributions, then the d.f. of the other distribution is given by the difference between the two.)
- The sum of the square of independent normal random variables has a chi-square distribution. Its degree of freedom is equal to the number of random variables. Or, in mathematical terms, if $Y = X_1^2 + \ldots X_n^2$ where $X_i \sim N(0, 1)$, then $Y \sim X_n^2$. Proof of this is accomplished by algebraically manipulating $P(Z^2 \leq w)$ until it becomes $2P(0 \leq Z \leq \sqrt{w})$ and then integrating the normal distribution's density function.
Critical value
$$P(X > \chi_{\alpha, n}^2) = \alpha$$
Insert diagram later
1.1.2The t-distribution¶
Density function
The density function of a random variable $T$ with a $t$-distribution with $n$ degrees of freedom ($n \geq 1, T \sim t_n$) is given by:
$$f(t) = \frac{\Gamma(\frac{n+1}{2})}{\sqrt{\pi n}\Gamma(\frac{n}{2})}\left ( 1 + \frac{t^2}{n} \right )^{-\frac{n+1}{2}}$$
Graph

Notice that as $n \to \infty$, the graph looks more and more like the normal distribution (the one in black).
Properties
None at the moment
Relation to other distributions
If $X \sim N(0,1)$ and $Y \sim X_n^2$, then
$$T = \frac{X}{\sqrt{Y/n}}$$
gives us a $t$ distribution with $n$ degrees of freedom (same as as the $\chi^2$ distribution).
Critical value
$$P(T > t_{\alpha, n}^2) = \alpha$$
Insert diagram later
1.1.3The F-distribution¶
Density function
The density function of a random variable $Y$ with an $F$-distribution with $n_1$ numerator and $n_2$ denominator degrees of freedom ($n_1, n_2 \geq 1, Y \sim F_{n_1, n_2}$) is given by:
$$g(y) = \begin{cases} \frac{\Gamma(\frac{n_1+n_2}{2})}{\Gamma(\frac{n_1}{2})\Gamma(\frac{n_2}{2})} \left ( \frac{n_1}{n_2} \right )^{n_1/2} y^{n_1/2 - 1} \left ( 1 + \frac{n_1}{n_2} y \right )^{-\frac{n_1+n_2}{2}}, & \text{if } y > 0, \\ 0, & \text{if } y \leq 0 \end{cases}$$
Graph

Properties
- The reciprocal of an $F$-distribution with $n_1$ numerator and $n_2$ denominator df is also an $F$ distribution, but with $n_1$ denominator and $n_2$ numerator d.f. Mathematically: if $Y \sim F_{n_1,n_2}$, then $1 / Y \sim F_{n_2, n_1}$.
- The reciprocal of the critical value is also the critical value of what? Come back to this later
Relation to other distributions
If $X_1 \sim \chi^2_{n_1}$ and $X_2 \sim \chi^2_{n_2}$ are independent, then
$$Y = \frac{X_1/n_1}{X_2/n_2}$$
gives us an $F$-distribution with $n_1$ numerator and $n_2$ denominator degrees of freedom.
Critical value
$$P(Y > F_{\alpha, n_1,n_2}^2) = \alpha$$
Draw diagram later
1.1.4Distribution summary table¶
Below is an overview of the above distributions (and the normal distribution), presented in tabular form:
| Distribution | Formula | d.f. | Properties | Relation to others |
|---|---|---|---|---|
| Normal - $N(\mu,\sigma^2)$ | $\displaystyle \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}\left (\frac{x-\mu}{\sigma} \right)^2}$ | N/A | $E(X) = \mu$, $Var(X) = \sigma^2$, $M_X(t) = e^{\mu t + \frac{1}{2}\sigma^2t^2}$ | N/A |
| Chi-square - $\chi^2_n$ | $\displaystyle\frac{1}{2^{n/2}\Gamma(n/2)}x^{n/2-1}e^{-x/2}$, $x > 0$ | $n$ | $E(X) = n$, $Var(x) = 2n)$, $M_X(t) = \frac{1}{(1-2t)^{n/2}}$ | Special case of gamma distribution ($\alpha = n/2$, $\beta = 2$). Mapped to $N(0,1)$ by $\frac{X-n}{\sqrt{2n}}$. Sum of $\chi^2$ distributions is a $\chi^2$ distribution (d.f.: sum of d.f.s). Sum of square of normal distributions is a $\chi^2$ distribution (d.f.: number of random variables). |
| t - $t_n$ | $\displaystyle \frac{\Gamma(\frac{n+1}{2})}{\sqrt{\pi n} \Gamma(\frac{n}{2})} \left ( 1+ \frac{t^2}{n} \right )^{-\frac{n+1}{2}}$ | $n$ | As $n \to \infty$, looks more like $N(0, 1)$ | $\displaystyle T = \frac{X}{\sqrt{Y/n}}$ where $X \sim N(0,1)$ and $Y \sim \chi^2_n$ ($T \sim t_n$) |
| F - $F_{n_1, n_2}$ | $\displaystyle \frac{\Gamma(\frac{n_1+n_2}{2})}{\Gamma(\frac{n_1}{2})\Gamma(\frac{n_2}{2})} \left ( \frac{n_1}{n_2} \right )^{n_1/2} y^{n_1/2 -1} \left ( 1 + \frac{n_1}{n_2} y \right )^{-\frac{n_1+n_2}{2}}$, $y > 0$ | $n_1$ numerator, $n_2$ denominator | Reciprocal is also $F$, reverse the d.f. | $\displaystyle Y = \frac{X_1/n_1}{X_2/n_2}$ where $X_1 \sim \chi^2_{n_1}$, $X_2 \sim \chi^2_{n_2}$ ($Y \sim F_{n_1, n_2}$) |
1.2Applications of some distributions¶
First, we make note of the following lemma:
Let ${x_1, \ldots, x_n}$ and ${y_1, \ldots, y_n}$ be two sets of $n$ numbers each, and let $\bar x$ and $\bar y$ be the means of each respective set. Then
$$ \sum_{i=1}^n (x_i - c) (y_i - d) = \sum_{i=1}^n (x_i - \bar x)(y_i - \bar y) + n(\bar x - c)(\bar y - d)$$
for any numbers $c$ and $d$. If they happen to be equal, then we have the following special case:
$$\sum_{i=1}^n (x_i - \mu)^2 = \sum_{i=1}^n (x_i - \bar x)^2 + n(\bar x - \mu)^2$$
I'd imagine that $c = d = \mu$, but the choice of symbol here seems deliberate - a connection to the normal distribution perhaps? In any case, the above can be proved using simple algebraic manipulation.
1.2.1Sample mean and variance¶
Let's say we have $n$ independent random variables - $X_1,\ldots X_n$ - all having the same distribution, with a mean of $\mu$ and a variance of $\sigma^2$. We can define the terms sample mean and sample variance as follows:
$$\text{Sample mean } = \overline X = \frac{X_1 + \ldots X_n}{n}, \quad \text{Sample variance } = s^2 = \frac{1}{n-1} \sum_{i=1}^n (X_i - \overline X)^2$$
Now, these metrics possess some interesting properties that are independent of the specific distribution of the random variables:
1.2.1.1Expected value of the sample mean¶
$$E(\overline X) = E\left ( \frac{X_1 + \ldots + X_n}{n} \right ) = \frac{1}{n} E\left( \sum_{i=1}^n X_i \right) = \frac{1}{n} \sum_{i=1}^n E(X_i) = \frac{1}{n}\sum_{i=1}^n \mu = \frac{\mu n}{n} = \mu$$
where $E(X_i) = \mu$ comes from the fact that each random variable has a distribution with a mean of $\mu$.
1.2.1.2Variance of the sample mean¶
$$Var(\overline X) = Var\left ( \frac{X_1 + \ldots + X_n}{n} \right ) = \frac{1}{n^2} Var\left( \sum_{i=1}^n X_i \right) = \frac{1}{n^2}\sum_{i=1}^n Var(X_i) = \frac{1}{n^2}\sum_{i=1}^n \sigma^2 = \frac{\sigma^2 n}{n^2} = \frac{\sigma^2}{n}$$
where $Var(X_i) = \sigma^2$ comes from the fact that each random variable has a distribution with a variance of $\sigma^2$.
1.2.1.3Relation to the normal distribution¶
If the samples all have a normal distribution, then $\overline X \sim N(\mu, \sigma^2/n)$. This can be proven using moment-generating functions. (Later.)
If they have an $F$ distribution, then this is only approximately true when $n$ is large, by the central limit theorem.
1.2.1.4Expected value of the sample variance¶
First, recall that $Var(x) = E((x - \mu)^2)$. Then, we rewrite the lemma above with the thing we need on the right, we have:
$$\sum_{i=1}^n (X_i-\overline X)^2 = \sum_{i=1}^n (X_i - \mu)^2 - n(\overline X - \mu)^2$$
(Note the switched order.) Then, we can derive the expected value of the sample variance as follows:
$$\begin{align*}E(s^2) & = E \left (\frac{1}{n-1} \sum_{i=1}^n (X_i - \overline X)^2 \right ) = \frac{1}{n-1} E\left (\sum_{i=1}^n (X_i - \overline X)^2 \right) = \frac{1}{n-1} E\left ( \sum_{i=1}^n (X_i - \mu)^2 - n(\overline X - \mu)^2 \right ) \\ & = \frac{1}{n-1} \left ( \sum_{i=1}^n E((X_i - \mu)^2) - n(E(\overline X- \mu)^2) \right ) = \frac{1}{n-1} \left ( \sum_{i=1}^n Var(X_i) - n Var(\overline X) \right ) = \frac{1}{n-1} \left ( n \sigma^2 - n \cdot \frac{\sigma^2}{n} \right ) \\ & = \frac{1}{n-1} (n\sigma^2 - \sigma^2) = \frac{(n-1)\sigma^2}{n-1} \\ & = \sigma^2 \end{align*}$$
Which is, well, kind of beautiful imo.
1.2.1.5Correlation between the sample mean and the individual samples¶
Recall that the formula for covariance is:
$$Cov(X, Y) = E((X - E(X))(Y-E(Y)))$$
and that the following properties hold:
$$Cov(X, Y - Z) = Cov(X, Y) - Cov(X, Z) \quad Cov(X, X) = Var(X)$$
We can then show that the sample mean, $\overline X$, and the difference between the sample mean and an individual sample, $X_i - \overline X$, are uncorrelated:
$$\begin{align*}Cov(\overline X, X_i - \overline X) & = Cov(\overline X, X_i) - Cov(\overline X, \overline X) = Cov(\overline X, X_i) - Var(\overline X) = Cov\left (\frac{X_1 + \ldots + X_n}{n}, X_i \right) - \frac{\sigma^2}{n} \\ & = \frac{1}{n} Cov \left (\sum_{j=1}^n X_j , X_i \right ) - \frac{\sigma^2}{n} = \frac{Cov(X_i, X_i)}{n} - \frac{\sigma^2}{n} = \frac{Var(X_i)}{n} - \frac{\sigma^2}{n} = \frac{\sigma^2}{n} - \frac{\sigma^2}{n} \\ & = 0\end{align*}$$
(We use the fact that the samples are independent to deduce that $Cov(X_i, X_j)$ when $i \neq j = 0$, and so can simplify $\displaystyle Cov \left (\sum_{j=1}^n X_j , X_i \right )$ to $Cov(X_i, X_i)$.) This is also kind of pretty.
1.2.1.6Independence of the sample mean and sample variance¶
Apparently the fact that $\overline X$ and $X_i - \overline X$ are uncorrelated implies that they are also independent. I didn't think this was true in the general case - maybe it's only true when they have a bivariate normal distribution? In any case, if those two are independent, then so are $\overline X$ and $(X_i - \overline X)^2$, and so $\overline X$ and $s^2$ are independent.
1.2.1.7Relation to the chi square distribution¶
If the random samples come from a normal distribution, then the sample variance relates to the chi-square distribution as follows:
$$\frac{(n-1)s^2}{\sigma^2} \sim \chi^2_{n-1}$$
We can prove this using the previously used lemma. First, we rewrite the above statistic by substituting in the equation for $s^2$:
$$\frac{(n-1)s^2}{\sigma^2} = \frac{(n-1)}{\sigma^2} \frac{1}{n-1} \sum_{i=1}^n (X_i - \overline X)^2 = \frac{\displaystyle \sum (X_i - \overline X)^2}{\sigma^2}$$
Next, let's divide each side of the equals sign in the lemma by $\sigma^2$:
$$\frac{\displaystyle \sum (X_i-\overline X)^2 = \sum (X_i - \mu)^2 - n(\overline X - \mu)^2}{\sigma^2} \quad \therefore \frac{\displaystyle \sum (X_i - \overline X)^2}{\sigma^2} = \frac{\displaystyle \sum (X_i - \mu)^2}{\sigma^2} - \frac{n(\overline X- \mu)^2}{\sigma^2}$$
$$\therefore \sum_{i=1}^n \left ( \frac{(X_i - \overline X)^2}{\sigma^2} \right ) = \frac{\displaystyle \sum (X_i - \mu)^2}{\sigma^2} - \frac{(\sqrt{n} \cdot \overline X- \mu)^2}{\sigma^2} = \underbrace{\sum_{i=1}^n \left ( \frac{X_i - \mu}{\sigma^2} \right )^2}_{\chi^2_n} - \underbrace{\left ( \frac{\overline X- \mu}{\sigma^2/\sqrt{n}} \right )^2}_{\chi^2_1}$$
and since the term on the left is equivalent to the statistic we're looking at, it has a $\chi^2$ distribution with $n-1$ degrees of freedom (see the "relation to other distributions" section of the chi-square distribution).
(We know that the two terms are $\chi^2$ distributions because WHY??? Oh, is it because you're squaring things that involve normal distributions ... yeah probably.
1.2.1.8Relation to the t distribution¶
$$\frac{\overline X - \mu}{s/\sqrt{n}} \sim t_{n-1}$$
where $X \sim N(0, 1)$ and $Y \sim \chi^2_m$.
This can be derived simply by rewriting the above statistic. Except I don't actually know how to do this. But it's probably not important.
1.3Order statistics¶
The $k$th order statistic ($Y_k$) is the $k$th smallest value among the random sample $X_1, \ldots, X_n$ from a continuous distribution. If we let $\omega$ mean "outcome" (not really sure why this is significant), then if $X_1(\omega) = 5$, $X_2(\omega) = 10$, $X_3(\omega) = 1$ then $Y_1(\omega) = 1$, $Y_2(\omega) = 5$ and $Y_3(\omega) = 10$.
Density function
$$g_k(y) = \frac{n!}{(k-1)!(n-k)!} (F(y))^{k-1} f(y) [1-F(y)]^{n-k}$$
where $F(y)$ is the distribution function, $f(y)$ is the density function and $g_k(y)$ is the density function for the $k$th order statistic ($Y_k$). This is apparently proved using the trinomial distribution and taking the limit of the probability density as $h \to 0$.
1.3.1Sample median¶
Basically the value that is smack in the middle. So if there are 5 values then $Y_3$, if there are 6 then the mean of $Y_3$ and $Y_4$. Not going to define it mathematically because it's kind of obvious.
Density function
The density function for the sample median given an odd sample size of $2m+1$ is:
$$g_m(y) = \frac{(2m+1)!}{m!m!} (F(y))^m f(y) (1-F(y))^m$$
1.3.2Expected values and variance¶
To find the expected value of an order statistic, integrate the density function. Remember that $f(x)$, the density function, is the derivative of the distribution function lol lol lol
2Estimation¶
Given some value $x$ from a distribution $X$ which depends on a parameter $\theta$, there are two main methods by which we can draw some conclusions about $\theta$:
- Estimation
- guessing $\theta$
- Hypothesis testing
- we use $x$ to help us decide between two hypotheses about $\theta$ (either it's one thing, or it's not)
- Statistic
- A function of $X$; if used to estimate $\theta$, it is called an estimator ($\hat \theta$), and its value is called the estimate
Usually, $X$ will be a random sample ($X_1, \ldots, X_n$) and $\theta$ will be either a scalar value or a vector (e.g. $(\mu, \sigma^2)$).
Some commonly used estimators of $\mu$ and $\sigma^2$:
$$\hat \mu = \overline X = \frac{1}{n} \sum_{i=1}^n X_i, \quad \hat \sigma^2 = s^2 = \frac{1}{n-1}\sum_{i=1}^n (X_i - \overline X)^2$$
2.1Methods of estimation¶
In this section: how to derive a suitable estimator for some given parameter.
2.1.1Maximum likelihood estimation¶
Use the likelihood function $L(\theta)$, and choose the value of $\theta$ for which $L(\theta)$ is at a maximum (can be found by taking the log and determining where the derivative is equal to 0).
Note that for the normal distribution, the MLEs for $\mu$ and $\sigma^2$ are just the sample mean and variance, respectively.
Properties
- MLEs are not unique
- May not always exist (for example, the uniform density function's log likelihood function has a derivative of $\displaystyle \frac{n}{\theta}$, and so there is no value of $\theta$ such that the derivative is 0, since we know that $n > 0$)
- Invariance: if $\hat \theta$ is an MLE of $\theta$, then $f(\hat \theta)$ is an MLE of $f(\theta)$ where $f$ is some function
Examples
When $\theta = 0$, $x$ is always 2. Then $\theta = 1$, $x$ is sometimes 1 but usually 2. If we observe that $x = 1$, then the MLE of $\theta$ is 1; if we observe that $x=2$, then the MLE of $\theta$ is 0.
Another example (from the lecture notes)
- When $\theta = 0$, $P(X = 1) = 0.1, P(X = 2) = 0.4, P(X = 3) = 0.5$
- When $\theta = 1/4$, $P(X = 1) = 0.2, P(X = 2) = 0.4, P(X=3) = 0.4$
- When $\theta = 1/2$, $P(X=1) = 0, P(X=2) = 0.3, P(X=3) =0.7$
Consequently, when $x = 1$, the MLE of $\theta$ is $1/4$. When $x = 2$, the MLE of $\theta$ is either $0$ or $1/4$. When $x = 3$, the MLE of $\theta$ is 1/2$.
A solved example from the lecture notes using a continuous likelihood function, where the density function is given by
$$g_{\theta}(t) = \frac{1}{\theta} e^{-t/\theta} \quad \text{when } t > 0; 0 \text{ otherwise}$$
and we want to estimate $\theta$. First, we find the likelihood function:
$$L(\theta) = f_{\theta}(t_1, \ldots, t_n) = g_{\theta}(t_1) \times \ldots \times g_{\theta}(t_n) = \frac{1}{\theta^n}e^{-n\overline t/\theta}$$
when all $t_i > 0$ and 0 otherwise. We then take the logarithm of the above to get the log likelihood function:
$$\mathcal{L}(\theta) = \log L(\theta) = \log \left ( \frac{1}{\theta^n}e^{-n\overline t/\theta} \right ) = -\frac{n \overline t}{\theta} - n\log \theta$$
If we differentiate this with respect to $\theta$, we get
$$\mathcal{L}'(\theta) = \frac{n\overline t}{\theta^2} - \frac{n}{\theta} = \frac{n}{\theta} \left ( \frac{\overline t}{\theta} - 1 \right)$$
We see that if $\overline t = \theta$, then the derivative becomes 0, indicating that the MLE is $\hat \theta = \overline t$.
Similarly, if the likelihood function is
$$L(\theta) = \frac{n}{\theta} e^{-ny/\theta}$$
(when $y > 0$) then the derivative of the log likelihood function is
$$\frac{d}{d\theta} \left ( \log \left ( \frac{n}{\theta} e^{-ny/\theta} \right ) \right ) = \frac{d}{d\theta} \left ( \log(n) - \log(\theta) - \frac{ny}{\theta} \right ) = -\frac{1}{\theta} + \frac{ny}{\theta^2} = \frac{1}{\theta} \left ( \frac{ny}{\theta} - 1 \right )$$
so when $ny = \theta$, then the derivative is 0 and so the MLE of $\theta$ is $ny$.
Another example from the lecture notes, using the binomial distribution, whose likelihood function is given by
$$L(\theta) = \binom{n}{k} \theta^k(1-\theta)^{n-k}$$
where $\theta$ is what we usually call $p$ (i.e. the probability of "success"). We can find the MLE of $\theta$ by differentiating the log likelihood function:
$$\frac{d}{d\theta} (\log L) = \frac{d}{d\theta} \left ( \log \binom{n}{k} + k\log \theta + (n-k)\log(1-\theta)\right ) = \frac{k}{\theta} + \frac{n-k}{1-\theta} = \frac{k(1-\theta) - \theta(n -k}{\theta(1-\theta)} = \frac{k - n\theta}{\theta(1-\theta)}$$
we see that if $\displaystyle \theta = \frac{k}{n}$, then the derivative is 0 and so the MLE of $\theta$ is $\displaystyle \frac{k}{n}$.
2.1.2Method of moments¶
Based on the strong law of large numbers:
$$\frac{1}{n} \sum_{i=1}^n X_i^k \to \mu'_k \,\,\text{as } n \to \infty$$
where $X$ is a random sample and $\mu_k'$ is the $kth$ moment ($E(X^k)$). So if $n$ is large enough, we have that
$$m_k = \frac{1}{n} \sum_{i=1}^n X_i^k \approx \mu_k'$$
If we set them to be equal, then we can solve the equations for the first few moments until we are able to identify $\theta$ (or whatever the parameters are).
Examples
For the exponential distribution with mean $\theta$: $\mu_1' = \theta$, $m_1 = \overline X$ so $\hat \theta = \overline X$.
For the Bernoulli distribution with $P(x=0) = 1-\theta$ and $P(x=1 = \theta$, $m_1 = \frac{1}{n} \sum_{i=1}^n X_i = \overline X$ and $\mu_1' = \theta$, so again we have $\hat \theta = \overline X$.
For the gamma distribution with parameters $\alpha$ and $\beta$, recall that the probability density function is given by
$$f(x) = X_i = \frac{1}{\Gamma(\alpha)\beta^{\alpha}} y^{\alpha -1}e^{-y/\beta}$$
So $\mu_1' = E(X) = \alpha\beta$ and $\mu_2' = E(X^2) = E(X^2) - (E(X))^2 + (E(X))^2 = Var(X) + (E(X))^2 = \alpha\beta^2 + (\alpha\beta)^2 = \alpha\beta^2 + \alpha^2\beta^2 = \alpha\beta(1+\alpha)$.
We don't seem to know the moments (?) so we just let $\mu_1' = m_1 = \alpha\beta$ and $\mu_2' = m_1 = \alpha\beta(1+\alpha)$ and we obtain the following equations for $\alpha$ and $\beta$:
$$\hat \alpha = \frac{m_2}{m_2 - m_1^2} \quad \hat \beta = \frac{m_2 - m_1^2}{m_1}$$
2.1.3Bayesian estimation¶
Chapter 16 in the textbook.
In this case, $\theta$ is a random variable with a distribution called the prior distribution. This essentially means that we have some information about $\theta$ (perhaps we believe it to be around 0.50, or 0.01, or something) but there is some uncertainty, which we handle by treating $\theta$ as a random variable. For example, if we believe $\theta$ to be about 0.10, we may use the beta distribution as a prior, with $\alpha = 1$, $\beta = 9$ (as the mean of the beta distribution is given by $\mu = \alpha/(\alpha+\beta)$). The density function for $\theta$ would then just be the beta distribution with $\alpha = 1$, $\beta=9$.
We then define a "loss" function $L(\theta, \hat \theta)$ which gives the loss/penalty when the true value of the parameter is $\theta$ and our estimate is $\hat \theta$. Examples of loss functions: taking the difference between the two and squaring it (the squared loss function), taking the absolute value of the difference between the two.
Consequently, to estimate $\theta$, we minimise the expected value of the loss function by finding the optimal estimator, $\hat \theta = t(X)$. For example, for the squared loss function, the Bayes estimator for $\theta$ is given by
$$\hat \theta = t(x) = E(\theta|X = x)$$
that is, the expected value of $\theta$, given that $X = x$. This conditional probability, called the posterior density function, is calculated as follows
$$\phi(\theta|x) = \frac{f_{\theta}x(x) h(\theta)}{g(x)}$$
where $h(\theta)$ is the prior density/probability function of $\theta$ and $f_{\theta}(x)$ is the conditional density/probability function $f(x|\theta)$.
The textbook definition this is slightly different (though the same idea). If $L$ is the likelihood function and $g$ is the prior density function then the posterior density of $\theta | y_1, \ldots, y_n$ is given by
$$g^*(\theta | y_1,\ldots y_n) = \frac{L(y_1, \ldots, y_n | \theta) \times g(\theta)}{\displaystyle \int_{-\infty}^{\infty} L(y_1,\ldots,y_n |\theta) \times g(\theta)\,d\theta}$$
Usually, a Bayesian estimation question will involve finding the posterior distribution for $\theta$ given the prior distribution.
2.2Properties of estimators¶
Four important ways of measuring "goodness" of estimators - unbiasedness, efficiency, consistency, sufficiency.
2.2.1Unbiasedness and efficiency¶
Unbiased: if the expected value of $\hat \theta = \theta$. The bias is given by $B(\hat \theta) = E(\hat \theta) - \theta$. The mean square error is given by $MSE(\hat \theta) = E(\hat \theta - \theta)^2$, which we can rewrite in terms of the variance and bias of $\hat \theta$:
$$MSE(\hat \theta) = E((\hat \theta - \theta)^2) = \underbrace{E(((\hat \theta - E(\hat \theta)) + (E(\hat \theta) - \theta))^2)}_{\text{adding and subtracting } E(\hat \theta)} = Var(\hat \theta) + (B(\hat \theta))^2$$
$$\begin{align*} MSE(\hat \theta) & = E((\hat \theta - \theta)^2) = \underbrace{E(((\hat \theta - E(\hat \theta)) + (E(\hat \theta) - \theta))^2)}_{\text{adding and subtracting } E(\hat \theta)} = E((\hat \theta - E(\hat \theta))^2 + 2(\hat \theta - E(\hat \theta))\underbrace{(E(\hat \theta) - \theta)}_{B(\hat\theta)} + \underbrace{(E(\hat \theta) - \theta)^2}_{B(\hat\theta)^2}) \\ & = \underbrace{E((\hat \theta - E(\hat \theta))^2)}_{Var(\hat \theta)} + 2\underbrace{(\hat \theta - E(\hat \theta))}_{E(\hat \theta) - E(\hat \theta) = 0}B(\hat \theta) + (B(\hat \theta))^2 \\ & = Var(\hat \theta) + (B(\hat \theta))^2 \end{align*}$$
The standard error is the standard deviation of $\hat \theta$, that is, the square root of its variance.
The relative efficiency of $\hat \theta_1$ with respect to $\hat \theta_2$ is given by
$$\frac{E(\hat \theta_2 - \theta)^2}{E(\hat \theta_1 - \theta)^2}$$
(Basically the ratio of their MSEs - a lower MSE means the estimator is more efficient.) The higher this value is, the more efficient $\hat \theta_1$ is than $\hat \theta_2$. If both are unbiased, then their relative efficiency depends on their variance.
A minimum variance unbiased estimator is the unbiased estimator with the lowest variance. Note that there may be more than one, or there may be no unbiased estimator with minimum variance (not sure when this would happen?).
2.2.1.1Cramer-Rao inequality¶
Let $\hat \theta = t(X)$ be an estimator of $\theta$, and let $f_{\theta}(x)$ be the likelihood function. Then we have
$$Var(\hat \theta) \geq \frac{\phi'(\theta)|^2}{\displaystyle E\left (\frac{\partial \log (f_{\theta}(X))}{\partial \theta} \right )^2}$$
where $\displaystyle \phi(\theta) = E(t(X)) = \int t(x) f_{\theta}(x)\,dx$ is the bias function (if the estimator is not biased, this is equal to $\theta$, and so $\phi'(\theta) = 1$).
If $X$ is a random sample $X_1, \ldots, X_n$ from a distribution with probability or density function $f_{\theta}(x)$, then the denominator (which is incidentally called the Fisher information of the observation $X$) is multiplied by $n$ and the $X$ is replaced by $X_1$ (I'm assuming because they all have the same probability/density function).
This can be proved with the assistance of the Cauchy-Schwarz inequality, i.e. that $|Cov(U, V)|^2 \leq Var(U)Var(V)$ (which incidentally shows up in MATH 223 as well).
If and only if equality holds, then $\hat \theta$ is said to be an efficient estimator of $\theta$. Note that equality holds if and only if $\hat \theta$ and the derivative of the log likelihood function are linearly related, meaning that the likelihood function must be of the form $f_{\theta}(x) = h(x)c(\theta)e^{w(\theta)t(x)}$ where $w(\theta) = \int a(\theta)\,d\theta$ (terminology: of exponential type). Not sure how important this is or what this really means.
We can use this theorem to show that an estimator is an MVUE. Recall that an MVUE must be unbiased and must be efficient. For example, to show that the estimator $\hat \mu = \overline X$ where $X_1,\ldots\,X_n \sim N(\mu, \sigma^2)$ is an MVUE of $\mu$, we have to show that equality holds (since we've already shown in Sample mean and variance that $E(\overline X) = \mu$).
First, we find the log likelihood function:
$$\log g(x_1) = \log \left (\frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2\sigma^2} (y-\mu)^2} \right ) = \log\left ( \frac{1}{\sigma\sqrt{2\pi}} \right ) + \left ( -\frac{1}{2\sigma^2} (x_1-\mu^2)\right ) = -\log(\sigma\sqrt{2\pi}) - \frac{1}{2\sigma^2} (x_1-\mu)^2$$
Then we differentiate it with respect to $\mu$:
$$\frac{\partial \log g(x_1)}{\partial \mu} = \frac{\partial }{\partial \mu} \left ( -\log(\sigma\sqrt{2\pi}) - \frac{1}{2\sigma^2} (x_1-\mu)^2 \right ) = \frac{\partial }{\partial \mu} \left (-\frac{(x_1-\mu)^2}{2\sigma^2} \right ) = \frac{2(x_1-\mu)}{2\sigma^2} = \frac{x_1-\mu}{\sigma^2}$$
Now, the Fisher information in this case is
$$nE \left ( \frac{\partial \log g(X_1)}{\partial \mu}\right )^2 = nE\left ( \frac{x_1-\mu}{\sigma^2} \right )^2 = n \frac{E(x_1-\mu)^2}{\sigma^4} = \frac{nVar(X_1)}{\sigma^4} = \frac{n\sigma^2}{\sigma^4} = \frac{n}{\sigma^2}$$
Since $\overline X$ is unbiased, the numerator $\phi'(\mu) = 1$. Now, we know that the variance of $\overline X$ is $\frac{\sigma^2}{n}$, so we get
$$\frac{\sigma^2}{n} \text{ on the left and } \frac{1}{n/\sigma^2} = \frac{\sigma^2}{n} \text{ on the right. }\,\blacksquare$$
2.2.2Consistency¶
An estimator $\hat \theta$ given a random sample consisting of $n$ variables is consistent if it's unbiased and if it approaches $\theta$ as $n$ approaches infinity. Alternatively: its variance must approach 0 as $n \to \infty$ (proven by Chebychev's inequality).
Example: show that the sample variance $\displaystyle s^2 = \frac{1}{n-1}\sum (X_i-\overline X)^2$ (with random samples from $N(\mu, \sigma^2)$) is consistent for $\sigma^2$. To do this, we use the fact that $(n-1)s^2/\sigma^2$ has a chi-square distribution with $n-1$ degrees of freedom and variance $2(n-1)$. We can then rewrite the formula for the variance of $s^2$ as follows:
$$Var(s^2) = Var\left ( \frac{\sigma^2}{n-1} \cdot \frac{(n-1)s^2}{\sigma^2} \right ) = \left ( \frac{\sigma^2}{n-1} \right )^2 Var\left ( \frac{(n-1)s^2}{\sigma^2} \right ) = \frac{\sigma^4}{(n-1)^2} \cdot 2(n-1) = \frac{2\sigma^4}{n-1}$$
We then take the limit as $n \to \infty$:
$$\lim_{n\to\infty} \frac{2\sigma^4}{n-1} = 0$$
2.2.3Sufficiency¶
An estimator is sufficient if it uses all the useful information about $\theta$. There is a theorem we can use here (I remember using it for an assignment). Use the Neyman-Pearson factorisation criterion (?). I suppose this can be left for the HTSEFP.
Needs to be possible to factor it as
$$f_{\theta}(x) = g_{\theta}[t(x)]h(x)$$
For example, from the normal distribution, if $\sigma^2$ is known, then $\overline X$ is sufficient for $\mu$. We can prove this by first finding the likelihood function:
$$L(x_1, \ldots, x_n) = \prod_{i=1}^n \left ( \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2\sigma^2} (x_i-\mu)^2} \right ) = \frac{1}{(\sigma\sqrt{2\pi})^n} e^{-\frac{1}{2\sigma^2} \sum (x_i-\mu)^2}$$
We then use the lemma from section 1.2:
$$L(x_1, \ldots, x_n) = \frac{1}{(\sigma\sqrt{2\pi})^n} e^{-\frac{1}{2\sigma^2} \sum(x_i - \overline x)^2} \cdot \frac{1}{(\sigma\sqrt{2\pi})^n} e^{-\frac{n}{2\sigma^2} (\overline x - \mu)^2}$$
So we can split it up into the product of two functions, one of which $(h(x_1,\ldots,x_n)$) is a function of the individual random variables but does NOT contain the thing we're trying to estimate, the other of which ($g_{\mu}(\overline x)$) is a function of the estimator $\overline x$ and which CAN contain the thing we're trying to estimate.
$$\therefore g_{\mu}(\overline x) = \frac{1}{(\sigma\sqrt{2\pi})^n} e^{-\frac{n}{2\sigma^2} (\overline x - \mu)^2}, \quad h(x_1, \ldots, x_n) = \frac{1}{(\sigma\sqrt{2\pi})^n} e^{-\frac{1}{2\sigma^2} \sum(x_i - \overline x)^2}$$
Another example, when neither $\sigma^2$ nor $\mu$ are known, and we want to estimate both. We'd have to be able to split it up into the product of two functions, one of which ($h(x_1, \ldots, x_n)$) is a function of the individual random variables but does NOT contain either $\sigma$ or $\mu$, the other of which ($g_{\mu, \sigma^2}(s^2, \overline x)$) is a function of both estimators and CAN contain $\mu$ and $\sigma^2$ (but not the individual random variables). We can use the fact that
$$s^2 = \frac{1}{n-1} \sum_{i=1}^n (x_i - \overline x)^2 \quad \therefore \sum_{i=1}^n (x_i - \overline x)^2 = (n-1)s^2$$
to obtain
$$g_{\mu, \sigma^2}(s^2, \overline x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{n}{2\sigma^2} (\overline x - \mu)^2 - \frac{(n-1)s^2}{2\sigma^2}} \quad h(x_1,\ldots,x_n) = 1$$
and so the factorisation is complete.
2.2.4Exponential families¶
A family of density/probability functions is called exponential if it can be expressed in some form, whatever. Examples: normal, binomial. Uniform is not.
- use of order statistics?
2.3Minimum variance revisited¶
- We can reduce variance of an unbiased estimator by conditioning on a sufficient statistic
- MVUE must be a function of "the" sufficient statistic. Why "the"?
- Rao-Blackwell
- Lehmann-Scheffe
- What does it mean for a statistic to be complete?
- fuck this section, gotta cut your losses at some point
3Confidence intervals¶
Interval estimation (as opposed to point estimation, which is what was covered in the last section). If $\hat \theta$ is a point estimator, then the bound on the error of estimation is $b = 2\sigma_{\hat \theta}$. If $\hat \theta$ is unbiased, then Chebychev's inequality tells us that the probability that $\hat \theta $ and $\theta$ are at most $b$ apart is at least 0.75; if the distribution is normal, then the probability is at least 0.95.
For example, if we're given $n = 50$, $\overline x= 11.5$ and $s=3.5$, then our estimate for $\mu$ would be 11.5, and our bound on the error of estimation would be $2\sigma/\sqrt{n} = 2s/\sqrt{n} = 7/\sqrt{50} = 0.99$ (we can approximate $\sigma$ by $s$ since $n$ is large).
For interval estimation, we need to find an interval $[\theta_L, \theta_U]$ for which $P(\theta_L \leq \theta \leq \theta_U) = 1 - \alpha$ for a $(1-\alpha) \times 100\%$ confidence interval.
A confidence interval is derived by using a pivot, which is a random variable of the form $g(X, \theta)$ whose distribution does not depend on $\theta$ (what??) and where the function $g(x, \theta)$ is for each $x$ a monotonic function of the parameter $\theta$ (what does this mean??).
For example, for the normal distribution with $\sigma^2$ known, to find the confidence interval for $\mu$, we use the pivot
$$\frac{\overline X - \mu}{\sigma/\sqrt{n}}$$
Which has a normal distribution $N(0, 1)$. Why do we use that pivot???? Because it's a standard one? Central limit theorem? Okay let's assume that and stop panicking.
If $\sigma^2$ is unknown, then the pivot is
$$\frac{\overline X - \mu}{s/\sqrt{n}}$$
Which has a $t$ distribution with $n-1$ d.f.
If $\mu$ is unknown, and we want to find the confidence interval for $\sigma^2$:
$$\frac{(n-1)s^2}{\sigma^2}$$
which has a $\chi^2$ distribution with $n-1$ d.f. So the lower bound is $\displaystyle \frac{(n-1)s^2}{\chi^2_{\alpha/2, n-1}}$ and the upper bound is $\displaystyle \frac{(n-1)s^2}{\chi^2_{1-\alpha/2, n-1}}$
Examples
Given the random sample 785, 805, 790, 793, 802 from $N(\mu, \sigma^2)$. We don't know either $\mu$ or $\sigma^2$. To find a 90% confidence interval for $\mu$, we use the fact that
$$\frac{\overline X - \mu}{s/\sqrt{n}} \sim t_{n-1}$$
We need to find a number $\mu_U$ such that $P(\mu > \mu_U) = 0.05$. First, we figure out $\overline X$ and $s$:
$$\overline X = 795 \quad s = \sqrt{\frac{1}{n-1} \sum (X_i - \overline X)^2} = \frac{1}{2} \sqrt{(10^2 + 10^2 + 5^2 + 2^2 + 7^2)} = 8.34$$
Anyway, the critical value for $\alpha = 0.05$ is 2.132 (from the $t$-distribution table in the back of the exam/textbook, with 4 degrees of freedom). So
$$\frac{\overline X - \mu_L}{s/\sqrt{n}} = \frac{795 - \mu_L}{8.34 / \sqrt{5}} = 2.132$$
So the confidence interval is given by
$$795 \pm \frac{2.132 \times 8.34}{\sqrt{5}} = 795 \pm 7.95 = [787.05, 802.95]$$
To find one for $\sigma^2$, we use the fact that
$$\frac{(n-1)s^2}{\sigma^2} \sim \chi^2_{n-1}$$
From the table in the back of the textbook for chi square, with 4 degrees of freedom, the critical value for $\alpha = 0.05$ is 9.48773 (the lower bound). Since this distribution is not symmetrical, we also need the critical value for the upper bound: 0.710721. So the confidence interval is given by
$$\frac{(4 \times 69.5}{9.48733} \leq \sigma^2 \leq \frac{4 \times 69.5}{0.710721} = [29.3, 391.15]$$
For a binomial distribution:
$$\text{Lower bound } = \hat p - z_{\alpha/2} \sqrt{\hat p (1-\hat p)}{n} \quad \text{Upper bound } = \hat p + z_{\alpha/2} \sqrt{\hat p (1-\hat p)}{n}$$
where $p = \frac{x}{n}$ (number of successes over number of trials) and $z_{\alpha/2}$ comes from the normal distribution etc.
For the difference between the means of two normal distributions whose variances are known, the pivot is
$$\frac{\overline X_1 - \overline X_2 -(\mu_1 - \mu_2)}{\displaystyle \sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}}$$
so the bounds are
$$(\overline x_1 - \overline x_2) \pm \sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}} \times z_{\alpha/2}$$
If the variances are unknown, then we have to assume that the variances are the same, and use the pooled sample variance instead of $\sigma_1^2$ and $\sigma_2^2$:
$$s_p^2 = \frac{(n_1 - 1)s_1^2 +(n_2 - 1)s_2^2}{n_1+n_2+2}$$
The distribution of the pivot is $t$ with $n_1 + n_2 - 2$ degrees of freedom. The confidence interval is then given by
$$(\overline x_1 - \overline x_2) \pm \sqrt{\frac{s_p^2}{n_1} + \frac{s_p^2}{n_2}} \times t_{\alpha/2, n_1+n_2-2}$$
Numerical example: $\overline x_1 = 64$, $\overline x_2 = 69$, $s_1^2 = 52$, $s_2^2 = 71$, $n_1 = 11$, $n_2 = 14$ and we want to find the difference between the means, $\mu_1-\mu_2$. First, let's find the pooled sample variance:
$$s_p^2 = \frac{(11-1)(52) + (13)(71)}{11+14-2} = \frac{520+ 923}{23} = 62.74$$
Now let's find a 95% confidence interval, given that we have a $t$ distribution with 21 degrees of freedom. From the table in the back of the book we have $t_{0.025, 23} = 2.069$. So the confidence interval is given by
$$(\overline x_1 - \overline x_2) \pm t_{0.025, 23}\sqrt{\frac{s_p^2}{n_1^2} + \frac{s_p^2}{n_2^2}} = -5 \pm 2.069 \sqrt{\frac{62.74}{11} + \frac{62.74}{14}} = -5 \pm 6.60 = [-11.60, 1.60]$$
Confidence interval for the ratio of variances
Two normal distributions, means and variances unknown, we want to find the ratio $\sigma_1^2/\sigma_2^2$. The pivot is
$$\frac{s_2^2/\sigma_2^2}{s_1^2/\sigma_1^2}$$
which has an $F$ distribution (NOT SYMMETRICAL!!) with $n_2-1$ numerator and $n_1-1$ denominator degrees of freedom. The confidence interval is therefore given by
$$\text{Lower bound } = \frac{s_1^2}{s_2^2} F_{1-\alpha/2, n_2-1, n_1-1} \quad \text{Upper bound } = \frac{s_1^2}{s_2^2} F_{\alpha/2, n_2-1, n_1-1}$$
The fact that
$$F_{1-\alpha/2, n_2-1, n_1-2} = \frac{1}{F_{\alpha/2, n_1-1, n_2-1}}$$
(NOTE THE SWITCHED NUMERATOR AND DENOMINATOR D.F.) may be useful.
Difference between binomial parameters
$\hat p_1 = x_1/n_1$, $\hat p_2 = x_2/n_2$. The pivot used here is
$$\frac{\hat p_1 - \hat p_2 - (p_1 - p_2)}{\sqrt{\frac{p_1(1-p_1)}{n_1} + \frac{p_2(1-p_2)}{n_2}}} \sim N(0, 1)$$
where we estimate $p_1$ and $p_2$ under the square root sign using $\hat p_1$ and $\hat p_2$. The final confidence interval is given by
$$\hat p_1 - \hat p_2 \pm z_{\alpha/2} \sqrt{\frac{\hat p_1(1-\hat p_1)}{n_1} + \frac{\hat p_2(1-\hat p_2)}{n_2}}$$
Mean of an exponential distribution
$X_i$ is a random sample from an exponential distribution with mean $\theta$ ($n$ samples total), which we want to find a confidence interval for. Let the pivot be
$$\frac{2}{\theta} \sum_{i=1}^n X_i$$
which has a chi-square distribution with $2n$ degrees of freedom. So the confidence interval is
$$\left [\frac{2\sum x_i}{\chi^2_{\alpha/2, 2n}}, \frac{2\sum x_i}{\chi^2_{1-\alpha/2, 2n}} \right ]$$
Large samples
When the sample size is large, we can assume that
$$\frac{\hat \theta - \theta}{\sigma_{\hat \theta}} \sim N(0, 1)$$
where $\sigma_{\hat \theta}$ is the standard error (standard deviation of the estimator $\hat \theta$). So the confidence interval is
$$\hat \theta \pm z_{\alpha/2} \sigma_{\hat \theta}$$
Bayesian credible sets
Bayesian analog of confidence intervals. Do we need to know this?
4Theory of hypothesis testing¶
4.1Introduction and definitions¶
Two hypotheses: the null hypothesis $H_0$, and the alternative hypothesis $H_1$. We select a critical region $C$ of the sample space, and if the random variable's outcome is in $C$, then we reject $H_0$ and accept $H_1$; else, we accept $H_0$ and reject $H_1$.
Of course, it's possible that we will falsely reject or accept a hypothesis. If $H_0$ is true but we reject it, that's a type I error; if $H_1$ is true but we reject it, that's a type II error. Pretty easy to remember. The probability of making a type I error is $\alpha = P(X \in C|H_0 \text{ is true})$, the probability of making a type II error is $\beta = P(X \notin C|H_1 \text{ is true})$. The power of the test is $1-\beta$.
Binomial distribution example
7 marbles, $\theta$ are red and the rest are green. We randomly select 3 without replacement to try and test the hypotheses
$$H_0:\, \theta = 3 \quad H_1:\,\theta = 5$$
Our rule is, if 2 or more of the marbles are red, reject $H_0$ and accept $H_1$; otherwise, accept $H_0$ and reject $H_1$. Let's calculate $\alpha$ and $\beta$ for this test.
$\alpha$ is the probability that there are 3 red marbles in the urn and 1 green marble and that when we select 3, there are 2 or 3 red marbles in our sample. So we find the sum of the probabilities of selecting all reds and of selecting one green:
$$\text{All red } = \frac{3}{7}\cdot \frac{2}{6} \cdot \frac{1}{5} = \frac{1}{35} \quad \text{One green } = \frac{3 \times 4 \times 3 \times 2}{7 \times 6 \times 5} = \frac{12}{35} \quad \therefore \alpha = \frac{13}{35}$$
$\beta$ is the probability that there are 5 red marbles in the urn and 2 green marbles and that when we select 3, there is 1 red marble and 2 green marbles. In other words, we select all the green marbles. This probability is
$$\beta = 3 \cdot \frac{2}{7} \cdot \frac{1}{6} = \frac{1}{7} = \frac{5}{35}$$
so the power of the test is $\frac{30}{35}$. I should probably figure out how to use the binomial distribution formulas rather than trying to derive everything all the time from scratch.
If the hypotheses were instead
$$H_0:\, \theta \leq 3 \quad H_1:\,\theta > 3$$
then the hypotheses would be composite instead of simple. We would then have to calculate $\alpha$ and $\beta$ values for each possible value of $\theta$ ($\alpha(\theta), \beta(\theta)$). The power function of the test (same as regular power, just, it depends on the value of $\theta$) is given by:
$$P(\theta) = P_{\theta}(\text{reject }H_0) = \begin{cases} \alpha(\theta) & \text{if we assume } H_0 \\ 1 - \beta(\theta) & \text{if we assume } H_1 \end{cases}$$
The size of the test is the maximum value of $\alpha(\theta)$; the level of the test is the maximum value of $\alpha$. Apparently the terms are used confusingly in the textbook.
Anyway, for this situation, we can construct a table for the power function (remember that the rule is to reject $H_0$ if there are 2 red marbles in the sample):
| $\theta$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| $P(\theta)$ | 0 | 0 | $\frac{1}{7}$ | $\frac{13}{35}$ | $\frac{22}{35}$ | $\frac{30}{35}$ | 1 | 1 |
Normal distribution example
We have a sample of size 10 from a distribution with variance $\sigma^2=625$. The hypotheses are:
$$H_0:\,\mu = 100 \quad H_1:\, \mu = 70$$
Rule: reject $H_0$ if $\overline X < 80$. Let's calculate $\alpha$ and $\beta$.
$\alpha$ is the probability that $\mu = 100$ and $\overline X < 80$. We can use the fact that
$$\frac{\overline X - \mu}{\sigma/\sqrt{n}} \sim N(0, 1)$$
for this:
$$\alpha = Pr_{H_0}\{X \in C\} = Pr_{\mu = 100} \{\overline X < 80 \} = Pr \left \{ \frac{\overline X - \mu}{\sigma/\sqrt{n}} < \frac{80 - 100}{25/\sqrt{10}} \right \} = Pr \{ Z < -2.53 \} = 0.0057$$
(using the table at the back of the book). To calculate $\beta$:
$$\beta = Pr_{H_1} \{X \notin C\} = Pr_{\mu = 70} \{ \overline X \geq 80 \} = Pr \left \{ \frac{\overline X - \mu}{\sigma/\sqrt{n}} \geq \frac{80 - 70}{25/\sqrt{10}} \right \} = Pr \left \{ Z > 1.26 \right \} = 0.1038$$
If we wanted to test the composite hypotheses
$$H_0:\, \mu \geq 100 \quad H_1:\,\mu < 100$$
it would be the same idea, except we'd have to do it for every possible value of $\mu$, which I don't think is important.
If we wanted to find a critical region of a size $\alpha$, we use
$$\frac{k - \mu}{\sigma/\sqrt{n}} = -z_{\alpha}$$
and solve for $k$ (which is the discriminant for the critical region). This gives us a new test and we can figure out the power for that.
4.2Choosing the critical region¶
4.2.1Simple hypotheses¶
First, we decide on a value of $\alpha$ (the level). Then, we choose the test that has maximum power for that level (i.e. we minimise $\beta$). This is called a most powerful test (critical region) of level $\alpha$.
For example, if $f_0(x)$ is the likelihood function of observation $X$ under hypothesis $H_0$ and $f_1(X)$ is the likelihood function of observation $X$ under hypothesis $H_1$ then, given a table or something, we can figure out the most powerful critical region for a given $\alpha$ level. Basically, we identify all those regions of size $\alpha$ or less, then find the power ($1-\beta$) for each region. Note that there can be a more powerful critical region with a smaller size, which is why we use levels etc.
How we do choose a most powerful critical region? We can use the Neyman-Pearson lemma:
Let $C$ be a critical region of size $\alpha$. If there exists a positive constant $k$ such that
$$f_0(x) \leq kf_1(x) \text{ when } x \in C \text{ and } f_0(x) > kf_1(x) \text{ when } c \notin C$$
then $C$ is a most powerful critical region of level $\alpha$.
Using this lemma, we can construct a most powerful region of size $\alpha$ (which will be the most powerful test of level $\alpha$).
Normal distribution example
Known variance of $\sigma^2$, random sample of size $n$, we want to test
$$H_0:\, \mu = \mu_0 \quad H_1: \,\mu=\mu_1$$
where $\mu_1 < \mu_0$. How do we find the most powerful critical region of size $\alpha$?
First, we find the likelihood function:
$$f_{\mu}(x) = f(x_1,\ldots\,x_n) = \prod_{i=1}^n \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2\sigma^2} (x_i-\mu)^2} = \frac{1}{(\sigma \sqrt{2n})^n} e^{-\frac{1}{2\sigma^2} \sum (x_i - \mu)^2} = \frac{1}{(\sigma\sqrt{2\pi})^2} e^{-\frac{1}{2\sigma^2}[\sum (x_i - \overline x)^2 + n(\overline x - \mu)^2]}$$
(making use of the lemma from section 1.2). Then we take the ratio of the hypotheses' likelihood functions:
$$\begin{align*} \frac{f_0(x)}{f_1(x)} & = \frac{1}{(\sigma\sqrt{2\pi})^2} e^{-\frac{1}{2\sigma^2}[\sum (x_i - \overline x)^2 + n(\overline x - \mu_0)^2]} / \frac{1}{(\sigma\sqrt{2\pi})^2} e^{-\frac{1}{2\sigma^2}[\sum (x_i - \overline x)^2 + n(\overline x - \mu_1)^2]} = e^{-\frac{1}{2\sigma^2}[\sum (x_i - \overline x)^2 + n(\overline x - \mu_0)^2] + \frac{n}{2\sigma^2}[\sum (x_i - \overline x)^2 + n(\overline x - \mu_1)^2]} \\ & = e^{\displaystyle -\frac{n}{2\sigma^2}[(\overline x - \mu_0)^2 - (\overline x - \mu_1)^2]} = e^{\displaystyle \frac{n(\mu_0-\mu_1)}{2\sigma^2}[2\overline x - (\mu_0 + \mu_1)]} \end{align*}$$
If we take the log of the above and periodically replace the term on the right by $k'$ etc (an arbitrary constant) we see that the critical region is given by
$$C = \left \{ \frac{f_0(x)}{f_1(x)} \leq k \right \} = \left \{ \frac{n(\mu_0-\mu_1)}{2\sigma^2}[2\overline x - \mu_0 - \mu_1] \leq \log k \right \} = \{ 2\overline x - \mu_0 - \mu_1 \leq k' \} = \{ \overline x \leq k'' \}$$
(Note that to get the first $k'$, we divided both sides by the fraction on the left, and since $\mu_1 < \mu_0$, this cannot be 0, so it's all valid etc.)
Anyway, we use $\displaystyle \frac{\overline X - \mu}{\sigma/\sqrt{n}}$ as usual, resulting in
$$Pr \left \{ Z \leq \frac{k'' - \mu_0}{\sigma/\sqrt{n}} \right \}$$
which implies that
$$\frac{k''-\mu_0}{\sigma/\sqrt{n}} = -z_{\alpha}$$
and so the value we use for the critical region is
$$\mu_0 - z_{\alpha} \frac{\sigma}{\sqrt{n}}$$
Or, we could calculate
$$z = \frac{\overline x- \mu_0}{\sigma/\sqrt{n}}$$
and reject $H_0$ at level $\alpha$ if $z \leq -z_{\alpha}$.
What if we wanted to test hypotheses involving $\sigma^2$? The derivation is similar, and the ratio of the two likelihood functions becomes
$$\frac{f_{\sigma^2_0}(x)}{f_{\sigma_1^2}} = \left ( \frac{\sigma_1^2}{\sigma_0^2} \right )^{n/2} e^{-\frac{1}{2}(\sigma_0^{-2} - \sigma_1^{-2} ) \sum (x_i-\mu)^2}$$
Let's use $\hat \sigma^2$ to estimate the variance:
$$\hat \sigma^2 = \frac{1}{n} \sum_{i=1}^n (x_i-\mu)^2$$
So we reject $H_0$ at level $\alpha$ if
$$\frac{n\hat\sigma^2}{\sigma_0^2} \geq \chi^2_{\alpha, n}$$
Binomial distribution example
We want to test
$$H_0:\,\theta = \theta_0 \quad H_1:\,\theta=\theta_1$$
The likelihood function for a binomial distribution is
$$f_{\theta}(x) = \binom{n}{x} \theta^x (1-\theta)^{n-x}$$
The derivation is pretty long and messy but in the end you choose the smallest $k$ such that $P(X \geq k) \leq \alpha$ or $P(X < k) \geq 1-\alpha$. (We choose the "smallest" to maximise the power). We'd have to use the binomial tables at the back of the book to find the actual value of $k$. For a numerical example, let $n = 20$, $\alpha = 0.05$, and we want to test $H_0: \theta = 0.3$ against $H_1: \theta = 0.5$. We need to find the smallest value of $k$ such that $P(X < k) \geq 1 - \alpha$, which is 0.95. We see that $P(X < 10) = 0.952$, so, $k$ is 10.
4.2.2Composite hypotheses¶
A test is uniformly most powerful if it is more powerful than any other test of level $\alpha$. Although these tests do not always exist, there is a method of finding them when they do, called the likelihood ratio method. It's basically the same as before, except you use the maximum possible value of $\theta$ for that hypothesis?
Normal distribution example
Random sample of size $n$ from a normal distribution where $\sigma^2$ is known. We want to test
$$H_0:\,\mu=\mu_0 \quad H_1:\,\mu\neq \mu_0$$
Skipping the derivation, we have that
$$z = \frac{\overline x - \mu_0}{\sigma/\sqrt{n}}$$
and we reject $H_0$ is $|z| \geq z_{\alpha/2}$.
There were a bunch of optional examples skipped at the end of this section.
4.3Hypothesis testing examples¶
Recall that $H_0$ is the null hypothesis, i.e. the "normal state of affairs". $H_1$ is the hypothesis which has the burden of proof on it, so that we only accept it if there is sufficient evidence for it. $H_1$ is therefore the statement to be proved, and the probability that we mistakenly accept $H_1$ is $\alpha$.
4.3.1p-levels¶
The p-level or (p-value) of a test is the value $\alpha$ that discriminates between rejecting $H_0$ and accepting $H_0$. Also called the observed/attained level of significance. Example:
$$H_0: \,\mu < 3.5 \quad H_1:\, \mu \geq 3.5$$
where $n = 50$, $\overline X = 3.3$ and the sample standard deviation $s = 1.1$ (since $n$ is large, we take $s = \sigma$). First, at $\alpha = 0.05$ (note $z_{\alpha} = 1.645$), what can we conclude? The formula is
$$z = \frac{\overline X - \mu}{\sigma/\sqrt{n}} = \frac{3.3 - 3.5}{1.1/\sqrt{50}} = -1.286$$
We reject $H_0$ only if $z$ is less than $-z_{\alpha} = -1.645$. It's not, so we don't reject it. However, if $\alpha$ were $0.10$, then $z_{\alpha} = 1.282$, so we could reject it with 80% confidence. Or is it 90%?
The $p$-value is essentially the probability that we are wrong. To calculate the $p$-value, we just use the equation
$$-1.286 = -z_{\alpha}$$
so $p = P(Z > 1.286) = 0.0992$.
We can also find the probability of making a type II error (i.e. the power of the test) for a given value of $\mu$. That is, we find the probability of rejecting $H_1$ (falling outside the critical region) when $H_1$ is true. For example, if $\mu = 3.4$, we first find the critical region:
$$\overline x < \mu - z_{\alpha}\frac{\sigma}{\sqrt{n}} = 3.5 - 1.645 \frac{11}{\sqrt{50}} = 3.244$$
so the probability of it falling outside the critical region given that $\mu = 3.4$ is given by
$$\begin{align*} \beta & = P_{\mu = 3.4} [ \overline X \geq 3.244 ] = P\left (Z \geq \frac{3.244 - 3.4}{1.1/\sqrt{50}} \right ) = P(Z \geq -1.003) \\ & = 1-P(Z < -1.003) = 1- P(Z > 1.003) = 1 - 0.1579 = 0.8421\end{align*}$$
So the power is $1-\beta = 0.1579$. Not really sure about this part.
Note that the "some last topics" section is optional which means I will ignore it
There are some examples here - should probably be in the HTSEFP or formulas to memorise
5Applications of hypothesis testing¶
5.1The bivariate normal distribution¶
Two random variables $X$, $Y$ have a bivariate normal distribution if their joint density function is some really long thing. Does this matter? $\rho$ is one of the parameters, and $Cov(X, Y) = \rho \sigma_1\sigma_2$.
5.2Correlation analysis¶
Whatever, not worth it
that's all for section 5 (ignore the bit at the end)
6Linear models¶
6.1Linear regression¶
Equation for the line of best fit: $y = \beta_0 + \beta_1 x$. However, since the points might not fall exactly on the line, we also have an equation for the relationship between $x_i$ and $y_i$ for the $i$th point:
$$y_i = \beta_0 + \beta_1 x_i + e_i$$
where $e_i$ is the "error" (the vertical distance of the point from the line). This chapter will be about using the data $(x_1, y_1),\ldots, (x_n, y_n)$ to estimate the parameters $\beta_0$ and $\beta_1$.
Actually, I seem to remember doing this in Calc A. The derivation is probably not important, so here's the gist: the values we need are
$$\sum x_i \quad \sum y_i \quad \sum x_i y_i \quad \sum x_i^2 \quad \sum y_i^2$$
The solutions are
$$\hat \beta_0 = \frac{(\sum x_i^2)(\sum y_i) - (\sum x_i )(\sum x_i y_i)}{n\sum x_i^2 - (\sum x_i)^2} \quad \hat \beta_1 = \frac{n(\sum x_i y_i) - (\sum x_i)(\sum y_i)}{n\sum x_i^2 - (\sum x_i)^2}$$
MEMORISE THESE. Just do it
Anyway, the values of $\beta_0$ and $\beta_1$ that we just got are estimates. It would be nice to be able to obtain confidence intervals and test hypotheses for these values. To be able to do that, we make certain assumptions:
- $x_i$'s are fixed (not the values of random variables)
- $x_i$ and $y_i$ are related by $y_i = \beta_0 + \beta_1 x_i + e_i$ where $e_i \sim N(0, \sigma^2)$ (the random variable)
Since there's a distribution involved, we can use another method to estimate $\beta_0$ and $\beta_1$: maximum likelihood estimation. First, we find the likelihood function by letting $\mu = y_i - \beta_0 - \beta_1 x_i$, and placing that into the formula for the normal distribution:
$$\prod_{i=1}^n \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2\sigma^2} (x_i - y_i + \beta_0 + \beta_1x_i)^2}$$
(this differs from the one given in the notes - mistake on my part or typo in the notes?) and by taking the log derivatives we see that we can get the same estimates for $\beta_0$ and $\beta_1$. Which is kind of neat.
6.1.1Finding distribution for the betas¶
$$\hat \beta_1 \sim N\left (\beta_1, \frac{\sigma^2}{n(\sum x_i^2) - (\sum x_i)^2} \right) \quad \hat \beta_0 \sim N\left ( \beta_0, \sigma^2 \left [ \frac{1}{n} + \frac{\overline x^2}{n(\sum x_i^2) - (\sum x_i)^2} \right ] \right )$$
Also, their covariance is given by
$$Cov(\hat \beta_0, \hat \beta_1) = -\frac{\sigma^2 \overline x}{n(\sum x_i^2) - (\sum x_i)^2}$$
so the estimated line $y = \hat \beta_0 + \hat\beta_1 x$ has distribution
$$\hat beta_0 + \hat \beta_1 x \sim N\left ( \beta_0 + \beta_1 x, \sigma^2 \left [ \frac{1}{n} + \frac{(x-\overline x)^2}{n(\sum x_i^2) - (\sum x_i)^2} \right ] \right )$$
(Derivations omitted)
Now, let $y = \hat \beta_0 + \hat\beta_1 x + e$ be the value resulting from some measurement, and let $\hat y = \hat \beta_0 + \hat \beta_1x$ be our prediction for $y$. Now, $E(y - \hat y) = 0$ (because of the above) and the variance is given by
$$Var(y - \hat y) = Var(y) + Var(\hat y) - \underbrace{2Cov(y, \hat y)}_{0} = \sigma^2 + \sigma^2\left [\frac{1}{n} + \frac{(x - \overline x)^2}{n(\sum x_i^2) - (\sum x_i)^2} \right ]$$
Consequently, the difference between the estimate and the true value is given by
$$y - \hat y \sim N(0, \sigma^2 \left [ 1 + \frac{1}{n} + \frac{(x-\overline x)^2}{n (\sum x_i^2) - (\sum x_i)^2} \right ]$$
However, the value of $\sigma^2$ is not likely to be known, so we have to estimate it. Let's define a value called the least squares minimum by
$$SS(Res) = \sum_{i=1}^n (y_i - \hat \beta_0 - \hat \beta_1 x_i)^2 = S_{yy} - \hat \beta_1 S_{xy}$$
where $S_{xy}$ and $S_{yy}$ are (I think?)
$$S_{yy} = \sum_{i=1}^n (x_i - \overline x)^2 \quad S_{xy} = \sum_{i=1}^n (x_i - \overline x)(y_i - \overline y)$$
The following gives us a $\chi^2$ distribution, with $n-2$ d.f., independent of the betas:
$$\frac{SS(Res)}{\sigma^2} \sim \chi^2_{n-2}$$
So we can get an unbiased estimator of $\sigma^2$ with
$$\hat \sigma^2 = \frac{SS(res)}{n-2}$$
We can get a $t$ distribution with $n-2$ d.f. by manipulating some shit. We can get more $t$ distributions for other things. In any case, the following all have $t$ distributions with $n-2$ d.f.:
$$\frac{(\hat \beta_1 - \beta)\sqrt{S_xx}}{\hat \sigma} \quad \frac{\hat \beta_0 - \beta_0}{\hat \sigma \sqrt{\frac{1}{n} + \frac{\overline x^2}{S_xx}}} \quad \frac{\hat \beta_0 + \hat \beta_1 x - \beta_0 - \beta_1 x}{\hat \sigma\sqrt{\frac{1}{n} + \frac{(x-\overline x)^2}{S_xx}}} \quad \frac{y-\hat y}{\sigma \sqrt{1 + \frac{1}{n} + \frac{(x-\overline x)^2}{S_xx}}}$$
There are some numerical examples here - go through them later, maybe in the HTSEFP
6.2Experimental design¶
One-way analysis of variance (experiment designs involving a single factor)
6.2.1Completely randomised designs¶
Let's say we want to test the effects of $k$ different fertilisers on wheat. So we plant a certain number of wheat plants in a bunch of different plots for each type of fertiliser. The yield from each plot is dependent on the effect of the fertiliser used as well as on the random error for that plot.
Okay, fuck that, here's what goes in an ANOVA table:
| Source of variation | Degrees of freedom | Sum of squares | Mean square | F |
|---|---|---|---|---|
| Treatments | $k - 1$ | SS(Tr) | MS(Tr) | $F_{Tr}$ |
| Errors | $N - k$ | SS(E) | MS(E) | -- |
| Total | $N - 1$ | SS(T) | -- | -- |
There are $k$ treatments in total (e.g. fertilizers). There are $N$ test plots (or like, plant pots, or test tubes, or whatever). The sum of squares column is given as follows:
$$SS(Tr) = \sum_{i=1}^k \frac{x_i^2}{n_i} - \frac{x^2..}{N} \quad SS(E) = \sum_{i=1}^k\sum_{j=1}^{n_i} x_{ij}^2 - \sum_{i=1}^k \frac{x_i^2}{n_i} \quad SS(T) = SS(E) + SS(Tr)$$
Now, what the fuck does that all mean?
$$\begin{align*}SS(Tr) & = \sum \underbrace{\frac{(\text{sum of yields for this fertiliser})^2}{\text{number of plots for this fertiliser}}}_{\text{for all the fertilisers}} - \frac{(\text{sum of all yields})^2}{\text{total number of plots}} \\ SS(E) & = (\text{sum of all the yields})^2 - \sum \underbrace{\frac{(\text{sum of yields for this fertiliser})^2}{\text{number of plots for this fertiliser}}}_{\text{for all the fertilisers}}\end{align*}$$
The mean square column is as follows:
$$MS(Tr) = \frac{SS(Tr)}{k-1} \quad MS(E) = \frac{SS(E)}{N- k}$$
(basically you divide the sum of squares by the degrees of freedom)
The last column, $F_{Tr}$, is just $MS(Tr)$ divided by $MS(E)$. If this value is greater than $F_{\alpha, k-1, N-k}$ then we reject $H_0$ (no treatment effects, in this case).
In this situation, the things we would need to compute/note are:
- $k$: the number of fertilisers used
- $x_{1.}$: the sum of yields for fertiliser 1
- $x_{2.}$: the sum of yields for fertiliser 2
- $x_{3.}$: the sum of yields for fertiliser 3
- $x_{..}$: the sum of yields among all the fertilisers
- $n_1$: the number of plots used by fertiliser 1
- $n_2$: the number of plots used by fertiliser 2
- $n_3$: the number of plots used by fertiliser 3
- $N$: the number of plots used, total, among all the fertilisers
- $\displaystyle \sum_{i=1}^k \sum_{j=1}^{n_i} x_{ij}^2$: sum of the (yield)2 among all the plots
- $\displaystyle \sum_{i=1}^k \frac{x_{i.}^2}{n_i}$: sum of (sum of yields for this fertiliser/number of plots for this fertiliser)2 among all the fertilisers
omg done
Example
Number of minutes taken to drive along 4 routes on different days of the week (thing we're testing: route)
| -- | Route 1 | Route 2 | Route 3 | Route 4 |
|---|---|---|---|---|
| Monday | 22 | 25 | 26 | 26 |
| Tuesday | 26 | 27 | 29 | 28 |
| Wednesday | 25 | 28 | 33 | 27 |
| Thursday | 25 | 26 | 30 | 30 |
| Friday | 31 | 29 | 33 | 30 |
- $k = 4$
- $x_{1.} = 129$ (total for route 1)
- $x_{2.} = 135$ (total for route 2)
- $x_{3.} = 151$ (total for route 3)
- $x_{4.} = 141$ (total for route 4)
- $x_{..} = 556$ (total for all routes)
- $n = 5$ (number of trial things for each route, all the same)
- $\sum \sum x_{ij}^2 =15610$ (sum of the total-for-each-trip-squared values for all routes)
- $\sum x_{i.}^2/n_i = 15509.6$ (sum of total-for-each-route-squared, divided by 5)
- $SS(Tr) = 15509.6 - 556^2/20 = 15509.6 - 15456.8 = 52.8$ (sum of squares for treatment)
- $SS(E) = 15610 - 15509.6 = 100.4$ (sum of squares for errors)
- $SS(T) = 52.8 + 100.4 = 153.2$ (sum of squares, total)
- $MS(Tr) = 52.8 / 3 = 17.6$
- $MS(E) = 100.4 / 16 = 6.275$
- $F_{Tr} = 17.6 / 6.275 = 2.804$
The ANOVA table is:
| Source of variation | Degrees of freedom | Sum of squares | Mean square | F |
|---|---|---|---|---|
| Treatments | 3 | 52.8 | 17.6 | 2.804 |
| Errors | 16 | 100.4 | 6.275 | -- |
| Total | 19 | 153.2 | -- | -- |
The distribution is $F_{3, 16}$. At $\alpha = 0.05$, $F_{0.05, 13, 16} = $3.24$. Since $F_{Tr}$ does not exceed this, we can't reject the null hypothesis, which means the time taken could be independent of the route (either 90% or 95% certain - confirm).
6.2.2Randomised block designs¶
Assigned randomly within blocks. When you have extraneous factors that could introduce bias (confounding), e.g. terrain in the fertiliser example.
The most important thing here is that we have a new ANOVA table to force into your head. :( Here:
| Source of variation | Degrees of freedom | Sum of squares | Mean square | F |
|---|---|---|---|---|
| Treatments | $k - 1$ | SS(Tr) | MS(Tr) | $F_{Tr}$ |
| Blocks | $n - 1$ | SS(Bl) | MS(Bl) | $F_{Bl}$ |
| Errors | $(n-1)(k-1)$ | SS(E) | MS(E) | -- |
| Total | $nk - 1$ | SS(T) | -- | -- |
$n$ is the number of blocks, obviously. Everything else is a little bit different now:
$$SS(T) = \sum_{i=1}^k \sum_{j=1}^n \left (x_{ij} - \frac{x..}{kn} \right )^2 \quad SS(Tr) = n\sum_{i=1}^k \left ( \frac{x_i.}{n} - \frac{x..}{kn} \right )^2 \quad SS(Bl) = k\sum_{j=1}^n \left ( \frac{x_{.j}}{k} - \frac{x..}{kn} \right )^2 \quad SS(E) = \sum_{i=1}^k\sum_{j=1}^n \left ( x_{ij} - \frac{x_{i.}}{n} - \frac{x_{.j}}{k} + \frac{x..}{kn} \right )^2$$
The mean square column is pretty simple, just the sum of squares divided by the degrees of freedom for that row.
The last column is the mean square in that row divided by $MS(E)$. Only available for the first two row, obviously.
Now let's redo the table for the routes thing:
- $k = 4$, as before
- $x_{1.} = 129$ (total for route 1)
- $x_{2.} = 135$ (total for route 2)
- $x_{3.} = 151$ (total for route 3)
- $x_{4.} = 141$ (total for route 4)
- $x_{..} = 556$ (total for all routes)
- $x_{.1} = 99$ (total for Monday)
- $x_{.2} = 110$ (total for Tuesday)
- $x_{.3} = 113$ (total for Wednesday)
- $x_{.4} = 111$ (total for Thursday)
- $x_{.5} = 123$ (total for Friday)
- $n = 5$ (5 blocks, as in 5 days of the week)
- $SS(Tr) = 5 * (4 + 0.64 + 5.76 + 0.16) = 52.8$ WTF why is it the same lol lol
- $SS(Bl) = 4 * (9.3025 + 0.09 + 0.2025 + 0.0025 + 8.7025 = 73.2$
- $SS(E) = $ fuck this I'll calculate the total instead
- $SS(T) = 153.2$ so $SS(E) = 153.2 - 126 = 27.2$
| Source of variation | Degrees of freedom | Sum of squares | Mean square | F |
|---|---|---|---|---|
| Treatments | $3$ | 52.8 | 17.6 | 7.75 |
| Blocks | $4$ | 73.2 | 18.3 | 8.06 |
| Errors | $12$ | 27.2 | 2.27 | -- |
| Total | $19$ | 153.2 | -- | -- |
To reject the null hypothesis for treatments, the $F$ value must be greater than $F_{0.05, 3, 12} = 3.49$; since it is, we can reject it. To reject the null hypothesis for blocks, the $F$ value must be greater than $F_{0.05, 4, 12} = 3.26$; since it is, we can reject it too.
7Chi-square tests¶
What is a chi-square test?
7.1Independent binomial populations¶
$X_1,\ldots X_k$ observations from independent binomial distributions with different parameters. We want to test the hypotheses that either the values of $p$ are the same (or some given value) for each distribution, or not. Since $X_i$ is a binomial random variable, if $n_i$ is large enough, then
$$\frac{X_i - n_i p_i}{\sqrt{n_1 p_i(1-p_i)}} \sim N(0, 1)$$
and so
$$\frac{(X_i - n_ip_i)^2}{n_ip_i(1-p_i)} \sim \chi^2_{1}$$
and thus, if all $n_i$ are large enough ($\geq k$), then, by independence:
$$\sum_{i=1}^k \frac{(X_i - n_i p_i)^2}{n_ip_i(1-p_i)} \sim \chi^2_{k}$$
The $\alpha$-level test is: reject $H_0$ if $\chi^2 \geq \chi^2_{\alpha, k}$ where $\chi^2$ in this case is the value given by
$$\chi^2 = \sum_{i=1}^k \frac{(X_i - n_i p_{i, 0})^2}{n_ip_{i, 0}(1-p_{i, 0})}$$
where I think $p_{i, 0}$ means the value of $p$ that you think it is?
For example, we want to test
$$H_0: \, p_1 = p_2 = p_3 = 0.3 \quad H_1: \text{ not } H_0$$
at $\alpha = 0.05$ (so $p_{1, 0} = 0.3$ and $1 - p_{1, 0} = 0.7$). The observations are:
$$x_1 = 155 \quad x_2 = 118 \quad x_3 = 87 \quad n_1 = 250 \quad n_2 - 200 \quad n_3 = 150$$
so
$$\chi^2 = \left ( \frac{(155 - 250 \cdot 0.3)^2}{250 \cdot 0.3 \cdot 0.7} \right ) +\left ( \frac{(118 - 200 \cdot 0.3)^2}{200 \cdot 0.3 \cdot 0.7} \right ) + \left ( \frac{(87-150\cdot 0.3)^2}{150 \cdot 0.3 \cdot 0.7} \right ) = 258$$
This is greater than $\chi^2_{0.05, 3} = 7.81$, so we reject the null hypothesis $H_0$.
Alternatively, if we just want to test if the $p$s are equal (and don't know the actual value) then we have to estimate $p$ by the pooled estimate:
$$\hat p = \frac{x_1 + \ldots + x_k}{n_1 + \ldots + n_k}$$
Same ideas as before, except you lose a degree of freedom because the common value is estimated by $\hat p$. Not really sure how that works but okay.
In the previous example, we would estimate $p$ to be
$$\hat p = \frac{155 + 118 + 87}{250+200+150} = 0.6$$
and so the value $\chi^2$ becomes
$$\chi^2 = \left ( \frac{(155 - 250 \cdot 0.6)^2}{250 \cdot 0.6 \cdot 0.4} \right ) +\left ( \frac{(118 - 200 \cdot 0.6)^2}{200 \cdot 0.6 \cdot 0.4} \right ) + \left ( \frac{(87-150\cdot 0.6)^2}{150 \cdot 0.6 \cdot 0.4} \right ) = 0.75$$
This is less than $\chi^2_{0.05, 2} = 5.99$ so we cannot reject $H_0$. So it's not unlikely that all the $p$s are the same.
7.2Multinomial distributions¶
thank god almost done
Suppose the random vector $(X_1, \ldots, X_k)$ has the multinomial distribution
$$P(X_1 = x_1, \ldots, X_k = x_k) = \begin{cases} \frac{n!}{x_1!\ldots x_k!}p_1^{x_1} \ldots p_k^{x_k} & \text{ if } x_1 + \ldots + x_k = n \\ 0 & \text{ otherwise} \end{cases}$$
with parameters $n$ (positive) and $p_1, \ldots, p_k$. Then we have a statistic called Pearson's chi-square statistic, given by
$$\chi^2 = \sum_{i=1}^k \frac{(X_i - np_i)^2}{np_i}$$
As $n \to \infty$, this distribution tends to the chi-square distribution with $k-1$ degrees of freedom, so for large enough $n$ (i.e. $np_i \geq 5$) we can approximate it by that. (Apparently this works partly due to the central limit theorem. We lose a degree of freedom because of the sum of the p's.)
The tests are pretty much the same as before, except for the loss of a degree of freedom. For example:
| Door | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Number of rats which choose door | 23 | 36 | 31 | 30 | 30 |
Test the hypotheses:
$$H_0: \, p_1 = p_2 = p_3 = p_4 = p_5 = 0.2 \quad H_1: \, \text{not } H_0$$
using $\alpha = 0.01$.
First, we calculate $\chi^2$ (the total number of rats is $23+36+31+30+30 = 150$
$$\chi^2 = \left (\frac{(23-30)^2}{30} \right ) + \left (\frac{(36-30)^2}{30} \right ) + \left (\frac{(31-30)^2}{30} \right ) + \left (\frac{(30-30)^2}{30} \right ) + \left (\frac{(30-30)^2}{30} \right ) = \frac{49}{30} + \frac{36}{30} + \frac{1}{30} = \frac{86}{30} = 2.87$$
Now, $\chi^2_{0.01, 4} = 13.28$. So we can't reject the hypothesis based on the data provided (i.e. the data are not sufficient to show that the rats show a preference for certain doors).
Wow, that was cool.
Incidentally, we can use this statistic to test hypotheses for other types of distributions, too. We have "observed cell frequencies" and "expected cell frequencies". The statistic becomes
$$\chi^2 = \sum_{i=1}^k \frac{(n_i-e_i)^2}{e_i}$$
where $e_i$ is the number expected in that cell. Same $\chi^2_{k-1}$ distribution. This is pretty straightforward.
Note that for each independent parameter that is estimated from the sample data, the degrees of freedom drops by 1.
7.3Goodness of fit¶
Hypothesis testing, whether the hypothesised distribution is correct or not. Use the formula above. For example, we want to test if something fits a Poisson distribution with a value supplied for $\lambda$. We calculate the expected values (based on the Poisson distribution) for each value of $x$ - $n_i \cdot P(X = i)$ - then we just use Pearson's chi-square statistic with $k-1$ degrees of freedom. If $\chi_2 \ geq \chi^2_{\alpha, k-1}$ then we reject $H_0$. (We can combine cells or something. Not really sure when it's necessary or why it's done, but it's doable.)
If we just want to test whether it fits a Poisson distribution without a value for $\lambda$, then we estimate $\lambda$ with the sample mean $\overline x$. Then, same idea, and since we had to estimate one parameter we drop the d.f. by one more (so now it's $k-2$).
In any case, even if we can't reject $H_0$ (the fit hypothesis, not sure why it's not a null hypothesis ...), we can't actually accept it. All we can say is the distribution with whatever parameter provides a good fit to the data or that the data are not inconsistent with the assumption of a whatever distribution with whatever parameter.
An example ($n = 100, \alpha = 0.05$):
| Cell | # of hours | $n_i$ | $e_i$ |
|---|---|---|---|
| 1 | 0 - 5 | 37 | 39.34 |
| 2 | 5-10 | 20 | 23.87 |
| 3 | 10-15 | 17 | 14.47 |
| 4 | 15-20 | 13 | 8.78 |
| 5 | 20-25 | 8 | 5.32 |
| 6 | 25+ | 5 | 8.20 |
where the $e_i$s come from the exponential distribution, by integrating over the limits given in the "# of hours" column, where we estimate $\hat \theta = \overline x = 10$ (why is it that??? oh okay multiply the midpoint of the number of hours by $n_i$, with the last column pretended to be $25-30$). We then find the chi-square statistic:
$$\chi^2 = \sum_{i=1}^6 \left ( \frac{(n_i - e_i)^2}{n_i} \right ) = \frac{2.34^2}{37} + \frac{3.87^2}{20} + \frac{2.53^2}{17} + \frac{4.22^2}{13} + \frac{2.68^2}{8} + \frac{3.20^2}{5} = 5.84$$
Now, $\chi_{0.05, 4} = 9.49$ (4 degrees of freedom because, $k-1$, then subtract another 1 because of the estimated parameter) so we can't reject the hypothesis.
7.4Contingency tables¶
Example:
| -- | Low interest in mathematics | Average "" | High "" |
|---|---|---|---|
| Low ability in stats | 65 | 40 | 15 |
| Avg "" | 54 | 63 | 29 |
| High "" | 12 | 45 | 27 |
We want to test $H_0:$ ability in stats and interest in math are independent and $H_1:$ not $H_0$. So what we do first is calculate the row and column sums and write those down in the table margins:
| -- | Low interest in mathematics | Average "" | High "" | Row sums |
|---|---|---|---|---|
| Low ability in stats | 65 | 40 | 15 | 120 |
| Avg "" | 54 | 63 | 29 | 146 |
| High "" | 12 | 45 | 27 | 84 |
| Column sums | 131 | 148 | 71 |
Then we make an expected cell frequency table, where each cell is the product of its row and column sums, divided by $n$ (350 in this case):
| -- | Low interest in mathematics | Average "" | High "" |
|---|---|---|---|
| Low ability in stats | 44.91 | 50.74 | 24.34 |
| Avg "" | 54.65 | 61.74 | 29.62 |
| High "" | 31.44 | 35.52 | 17.04 |
Then we calculate the chi-square statistic:
$$\chi^2 = \sum_{i=1}^r \sum_{j=1}^c \frac{(n_{ij} - e_{ij})^2}{e_{ij}}$$
which is pretty much the same thing as before (remember to divide BY THE EXPECTED, as is usual). We then just compare it with $\chi^2_{\alpha, (r-1)(c-1)}$.
In this specific case it should be $\chi^2 = 35.26$, $\chi_{0.01, 4} = 13.28$ so we reject $H_0$ meaning they are probably not independent. The notes say $\chi^2 = 31.67$ but I think this is wrong?
8Non-parametric methods of inference¶
IGNORED THANK GOD

