Home MATH 340 Tuesday, February 4, 2014

Tuesday, February 4, 2014 CC-BY-NC
Planar duals

Maintainer: admin

1Planar duals

Any planar drawing $G$ has a corresponding a dual (also planar), which we'll call $H$.

To find the dual: draw the vertices for $H$ in the faces of $G$, and connect them if there's an edge between the faces.

Thus $V(H) = F(G)$, $E(H) = E(G)$ and $(f_1, f_2) \in E(H) \iff f_1, f_2$ are adjacent faces in $G$.

Incidentally, the dual of the octahedron is actually the graph of the cube. The dual of the icosahedron is the dodecahedron, and the dual of the tetrahedron is itself (wow).

Also, colouring a map is equivalent to colouring the dual of the graph.

Observe that the drawing of the dual graph, $H$, depends on the drawing of $G$. We define the term $k$-connected: a graph $G$ is $k$-connected if $\forall u, v, \in V(G)$, there exist at least $k$ vertex-disjoint paths between $u$ and $v$ (i.e., at least $k$ different ways of going from $u$ to $v$).

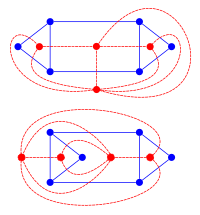
We claim that if $G$ is 3-connected and planar then it has a unique dual. On the other hand, if a graph is not 3-connected, it may have 2 or more dual graphs, depending on the way we draw the original graph.

For example:

A graph with multiple distinct duals

We can be certain that these are two different graphs (and not just the same graph drawn in a slightly different way) by looking at the distribution of degrees.

1.1Bipartite graphs and Eulerian duals

Theorem: $G$ is bipartite $\iff$ its dual $H$ is Eulerian.

Proof left as an exercise.

1.2Graph minors

We say $H$ is a minor of $G$ if it can be obtained from $G$ by applying a sequence of the following operations:

  1. Edge deletion: remove an edge $e$ ($G-e$)
  2. Vertex deletion: remove a vertex and all of its adjacent edges
  3. Edge contraction: contract an edge $e=(i, j)$ by combining $i$ and $j$ and removing loops and multiple edges ($G/e$).

If $H$ is a minor of $G$ we write $H \preccurlyeq G$. The minor property is transitive.

Suppose we're given a particular graph $H$ and we're trying to see if we can find it as as minor in $G$. The way to do this is to look for trees in $G$ that correspond to the vertices of $H$, and then just contract the trees. Note that they have to be trees, and not cycles; contracting cycles doesn't give you anything you couldn't get by contracting a tree.

1.2.1Kuratowski's theorem

Here's why minors are useful:

Theorem: $G$ is planar $\iff$ $G$ does not contain a $K_5$ minor or a $K_{3,3}$ minor.

Proof: By Euler's formula, if $G$ contains a $K_{3,3}$ or $K_5$ subgraph, then it is clearly not planar. Similarly, if they're contained as minors, then $G$ can't be planar either - for example, if $K_5$ is present as a minor, then $G$ has 5 trees, all of which are completely connected. (It seems obvious from this that $G$ is therefore not planar, but I'm not sure how to formalise that.)

Suppose, instead, that $G$ has neither a $K_5$ minor nor a $K_{3,3}$ minor. How can we show that $G$ is planar? (Note: this is probably one of the hardest theorems in the course.) We can prove this as follows: suppose the theorem is false. In that case, there must be at least one counterexample. Consider the smallest counterexample $G$ (so the smallest graph $G$ which has neither a $K_5$ nor a $K_{3,3}$ as a minor and yet is not planar). This will be a proof by contradiction, making use of the fact that any smaller graph is not a counterexample.

Take an arbitrary edge $e = (u, v)$ in $G$, and contract it to produce $G' = G\setminus e$. The resulting graph $G'$ is planar, since it has no $K_{5}$ or $K_{3,3}$ minor (by transitivity) and is smaller than $G$ (otherwise, it would contradict the fact that $G$ is the smallest counterexample).

Now let's add back $e$ to $G'$, which will give us a graph that is equivalent to the original $G$. We'll now show that the resulting graph $G$ is planar.

First, we show that $G$ is 4-connected. To do so, take any planar drawing of $G'$. Look at the face $F$ containing the contracted supernode $(u, v)$. I don't really understand the rest of this proof, so fuck it.

1.3The Hadwiger conjecture

$$\chi(G) \geq t \; \implies K_t \preccurlyeq G$$

So if I need $t$ colours to colour graph $G$, then $G$ contains a clique of size $t$ as a minor.

Remains an open problem. For $k=5$, this implies the four colour theorem, which is kind of neat.