Planar graphs. Euler's formula, and using the formula to find an upper bound for the number of edges in a planar graph. Platonic solids and their relation to planarity.
1Planar graphs¶
Note that we're only working with simple graphs at the moment - graphs where each pair of vertices has at most 1 edge between them.
A graph $G$ is planar if it can be drawn on a plane without any two edges crossing. Note that the edges don't have to be drawn as straight lines.
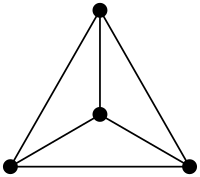
Recall that $K_n$ is the complete graph containing $n$ vertices. Now, $K_4$ is planar, though it might not be obvious at first. Here's $K_4$, drawn the standard way (which is not a planar drawing):
Here's a planar way of drawing $K_4$:
So $K_4$ is planar, as there's a way of drawing it on a plane without edges crossing.
What about $K_5$? Well, it doesn't seem planar. Can we prove that it isn't?
1.1Euler's formula¶
First, we introduce the term faces, which refers to the regions enclosed by the edges on the plane. We number the faces $F_1, \ldots, F_f$ where $f$ is the number of faces. Also, the "infinite" or "outer" face around the graph, we call $F_0$.
Let $n$ be the number of vertices, and let $m$ be the number of edges. Then:
Theorem (Euler, 1752): A connected planar graph satisfies $m+2 = n+f$.
Proof: by induction. First, note that the cheapest way to connect a graph of $n$ vertices is with a spanning tree, which requires $m=n-1$ edges. So let the base case be the connected spanning tree $T$ on $n$ vertices. It's easy to see that if we have a tree, we can draw the graph so that it is planar (recall that trees, by definition, do not have any cycles). There is only one face for a tree, so $f=1$. Thus, $m+2 = (n-1) + 2 = n+1 = n + f \checkmark$
For larger connected graphs, the graph must contain a cycle (otherwise, it's just a tree, which is the base case). Consider the graph $G' = G\setminus e$ where $e$ is some edge of (one of) the cycle(s). Then, for $G'$, the number of vertices is the same - so $n'=n$ - but the number of edges is one less than that of $G$, so $m' = m - 1$. Furthermore, the number of faces is one less as well, since by removing an edge, we merge two faces into one. Thus $f' = f-1$.
If we assume the induction hypothesis for $G'$, then we have:
$$\begin{align} & m' + 2 = n' + f' \\ \therefore \; & (m-1) + 2 = n + (f-1) \\ \therefore \; & m + 2 = n + f \; \blacksquare \tag{so the formula holds for $G$} \end{align}$$
A corollary of this theorem is that any drawing of a planar graph results in the same number of faces.
1.2Upper-bounding the number of edges¶
Another corollary of the previous theorem is that it allows us to find an upper bound for the number of edges in a planar graph.
Theorem: In any planar graph, $m \leq 3n - 6$ (for $n \geq 4$).
Note that in a general graph, the maximum number of edges is $\Omega(n^2)$ since $\displaystyle \binom{n}{2} = \frac{1}{2}n(n-1)$. This theorem establishes an even smaller upper bound, but only for planar graphs.
Proof: In a planar graph, each edge touches at most 2 faces1. The number of edges around a face is at least 3. Thus, if we count the number of pairs $(e, F)$ such that $e \in F$, then this number is at least $3f$, but is at most $2m$. So then we have that $2m \geq 3f$. By Euler's formula, we have that $m + 2 = n + f$. Thus $3m+6 = 3n+3f \leq 3n+2m$, and so $3m+6 \leq 3n+2m$. Subtracting $2m$ from both sides, we get $m+6 \leq 3n$ and so $m \leq 3n-6$, as desired. $\blacksquare$
1.2.1For bipartite graphs¶
Theorem: In a planar bipartite graph, $m \leq 2n-4$ (when $n \geq 5$).
Proof: In a planar bipartite graph, there are no odd cycles, so the smallest cycle has 4 edges. Thus, any face (other than the infinite one) has to have at least 4 edges around it. Other than that, the proof is similar to what we had before: $2m \geq$ the number of pairs $\geq 4f$, so $2m \geq 4f$, thus $m \geq 2f$. Using Euler's formula, we get $2m+4 = 2n+2f$ and so $2m+4 \leq 2n+m$. Subtracting $m$ from both sides, we get $m+4 \leq 2n$, and so $m \leq 2n-4$. $\blacksquare$
This gives us an upper bound on the density of planar graphs.
1.2.2Proving non-planarity¶
We can use the theorems above to prove that $K_5$ is not planar, as we suspected. For $K_5$, we have $n=5$ vertices, and $m=4+3+2+1=10$ edges. But $3n-6 = 9$ and $10 > 9$. Thus $K_5$ is not planar.
Similarly, consider $K_{3,3}$, the complete bipartite graph with 3 vertices in each bipartition. There are $n=6$ vertices, and $m = 9$ edges. But $2m-4=8$ and $9 > 8$. Thus $K_{3,3}$ is also not planar.
We'll show later that these two graphs - $K_{3,3}$ and $K_5$ - are the only reasons a graph would not be a planar, in the sense that any graph that is not planar must contain a copy of $K_5$ or $K_{3,3}$ within it somewhere.
1.3Platonic solids¶
A regular polytope is a 3D convex solid whose sides are formed by identical 2D regular polygons. Here's a table of the standard ones, where $d$ is the number of faces touching each vertex and $p$ is the number of sides for each face:
| Name | Drawing | Faces | Vertices | Edges | $p$ | $d$ |
|---|---|---|---|---|---|---|
| Tetrahedron |  |
4 | 4 | 6 | 3 | 3 |
| Cube |  |
6 | 8 | 12 | 4 | 3 |
| Octahedron |  |
8 | 6 | 12 | 3 | 4 |
| Dodecahedron |  |
12 | 20 | 30 | 5 | 3 |
| Icosahedron |  |
20 | 12 | 30 | 3 | 5 |
Are there any other platonic solids? To find out, let's consider these solids as planar graphs, by projecting them down to a 2D plane. I'm not entirely sure how the projection works, but I don't think that matters. This isn't MATH 350.
Image taken from Wolfram MathWorld, shown in the same order as in the table above
Note that each vertex has degree $d$ and each face has $p$ sides.
Theorem: The 5 platonic solids above are the only platonic solids.
Proof: We can derive this from Euler's formula. A regular polytope gives a regular planar graph with $\displaystyle 2m = \sum_{v \in V}\deg(v) = n\cdot d$ (since it's regular).
But each edge has exactly 2 faces. So $2m = f \cdot p$.
By Euler's formula, $m+2 = n+f$, thus
$$m+2 = \frac{2m}{d} + \frac{2m}{p}$$
Divide both sides by $2m$, and we get:
$$\frac{1}{2} + \frac{1}{m} = \frac{1}{d} + \frac{1}{p}$$
For 3d solids, we need $d \geq 3$ and $p \geq 3$. So what values of $p$ and $d$ work for this formula? Suppose $p \geq 4$ and $d \geq 4$. Is that possible? No, because then $\displaystyle \frac{1}{d} + \frac{1}{p} \leq \frac{1}{2} < \frac{1}{2} + \frac{1}{m}$ and there is no possible value of $m$ that could satisfy that equation (that also happens to be a valid number of edges). On the other hand, if $d = 3$, then $\displaystyle \frac{1}{2} + \frac{1}{m} = \frac{1}{3} + \frac{1}{p}$, i.e.,
$$\frac{1}{p} = \frac{1}{6} + \frac{1}{m}$$
Since $\frac{1}{m} > 0$, then $p < 6$, i.e., $p \leq 5$. So the only possible values for $(d, p)$ are $(3, 3)$, $(3, 4)$, $(3, 5)$, $(4, 3)$, and $(5, 3)$. Let's investigate the solids resulting from each of these values:
| $d$ | $p$ | $\displaystyle m = \left (\frac{1}{d} + \frac{1}{p} - \frac{1}{2} \right )^{-1}$ | $\displaystyle n = \frac{2m}{d}$ | $\displaystyle f = \frac{2m}{p}$ | Resulting solid |
|---|---|---|---|---|---|
| $3$ | $3$ | $6$ | $4$ | $4$ | Tetrahedron |
| $3$ | $4$ | $12$ | $8$ | $6$ | Cube |
| $3$ | $5$ | $30$ | $20$ | $12$ | Dodecahedron |
| $4$ | $3$ | $12$ | $6$ | $8$ | Octahedron |
| $5$ | $3$ | $30$ | $12$ | $20$ | Icosahedron |
So the solids we identified earlier are, in fact, the only ones!
-
An edge is always adjacent to at least one face, which may just be the infinite face. ↩